Fique por dentro das novidades
Inscreva-se em nossa newsletter para receber atualizações sobre novas resoluções, dicas de estudo e informações que vão fazer a diferença na sua preparação!
Questão ativa
Já visualizadas
Não visualizadas
Resolução pendente
Questão anulada
Sem alternativas

Uma bola é chutada obliquamente, no instante , com velocidade inicial , no ponto A de uma elevação. Essa bola descreve a trajetória indicada na figura passando pelo ponto B, ponto mais alto de sua trajetória, no instante t = 0,8 s, e atinge o solo horizontal no ponto C, no instante t = 2 s.
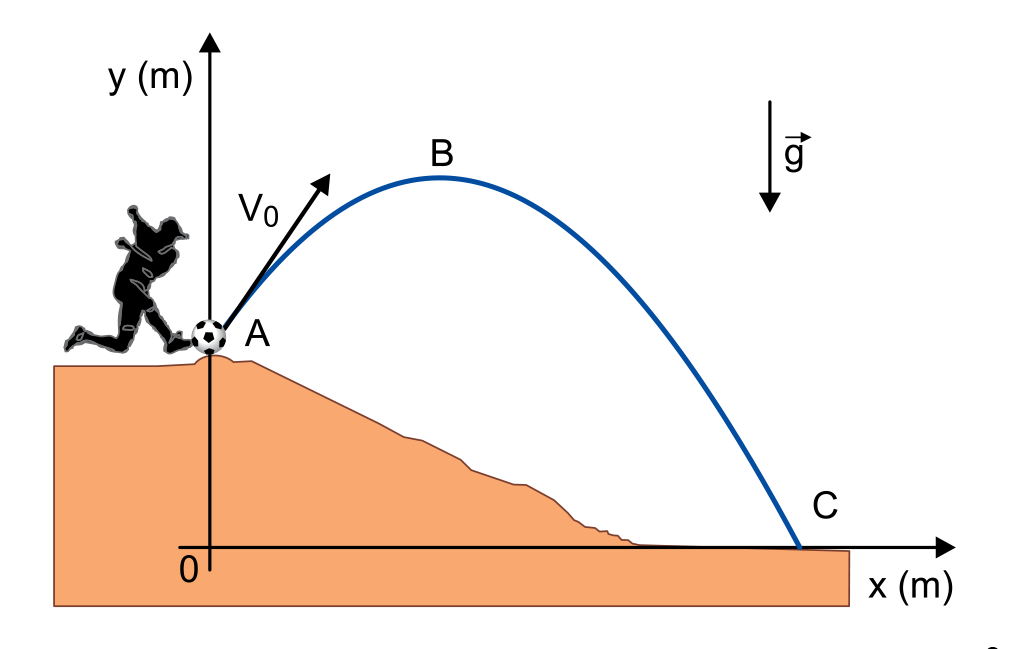
Desprezando a resistência do ar, adotando e sabendo que a equação da trajetória dessa bola, desde o ponto A até o ponto C, é , o módulo de é
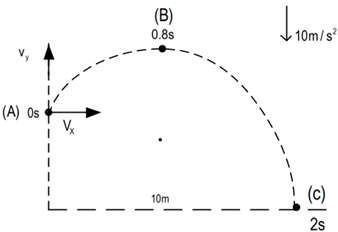
1) Cálculo de
2) Para
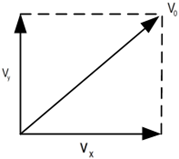
3) Cálculo de :
4)
Inscreva-se em nossa newsletter para receber atualizações sobre novas resoluções, dicas de estudo e informações que vão fazer a diferença na sua preparação!