Fique por dentro das novidades
Inscreva-se em nossa newsletter para receber atualizações sobre novas resoluções, dicas de estudo e informações que vão fazer a diferença na sua preparação!
Questão ativa
Já visualizadas
Não visualizadas
Resolução pendente
Questão anulada
Sem alternativas

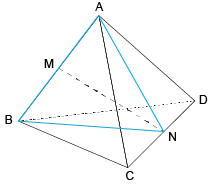
A figura abaixo indica um tetraedro regular ABCD de aresta 6 cm. M e N são pontos médios das arestas e , respectivamente.

Na situação descrita, a medida de , em centímetros, é igual a:
Considere o triângulo ABN, como indicado na figura a seguir:
Nota-se que, como N é o ponto médio do segmento CD, BN é a mediana do triângulo BCD relativa ao vértice B, mas como o triângulo BCD é equilátero, a mediana é igual a altura. Portanto, a medida do segmento BN é .
O mesmo ocorre com o segmento AN do triângulo ACD, ou seja, a medida do segmento AN é .
Como o triângulo ABN é isósceles, a mediana MN também é a altura do triângulo ABN relativa ao vértice N.
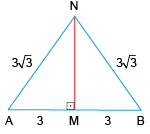
Pelo teorema de Pitágoras no triângulo AMN, tem-se:
Inscreva-se em nossa newsletter para receber atualizações sobre novas resoluções, dicas de estudo e informações que vão fazer a diferença na sua preparação!