Fique por dentro das novidades
Inscreva-se em nossa newsletter para receber atualizações sobre novas resoluções, dicas de estudo e informações que vão fazer a diferença na sua preparação!
Questão ativa
Já visualizadas
Não visualizadas
Resolução pendente
Questão anulada
Sem alternativas

Um engenheiro está projetando um trampolim para um parque aquático. O trampolim estará a 1 m de altura em relação ao nível da água da piscina. No ponto Q, o atleta iniciará seu salto, em trajetória parabólica até a altura máxima em R, iniciando sua trajetória descendente, passando por S e finalizando o salto entrando na água em T, como mostra a figura.
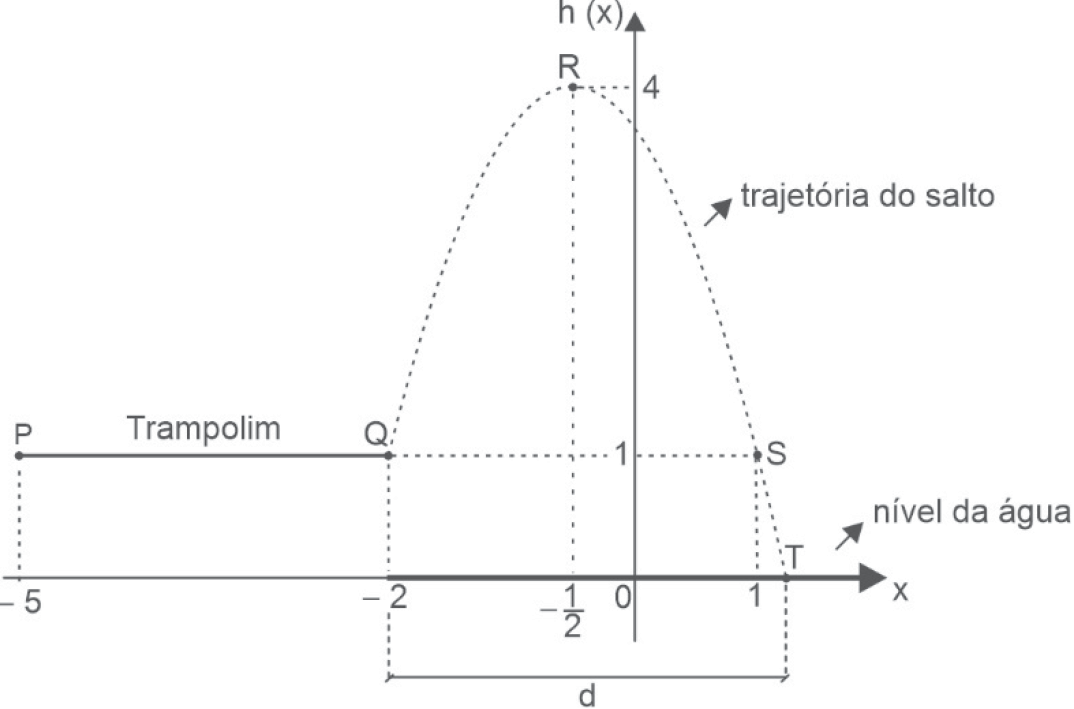
Se a trajetória do atleta no ar é modelada pela função quadrática , com h(x) e x em metros, a distância representada por d na figura, em metros, é igual a
A trajetória do salto é dada pela função e passa pelos pontos , e .
Substituindo as coordenadas desses pontos na função quadrática, obtém-se o seguinte sistema de equações:
Multiplicando a primeira linha por 4 e subtraindo da segunda linha, obtém-se:
Fazendo a primeira linha subtraída da terceira linha, obtém-se .
Fazendo a primeira linha subtraída da terceira linha , tem-se , e substituindo na terceira linha, obtém-se .
Portanto, a função quadrática é da forma .
As raízes dessa equação podem ser encontradas pela fórmula de Bhaskara:
e
A abscissa do ponto T representa a raiz positiva de h, assim, .
A distância d solicitada é .
Inscreva-se em nossa newsletter para receber atualizações sobre novas resoluções, dicas de estudo e informações que vão fazer a diferença na sua preparação!