unicamp

Dissertativa 5 - 2ª Fase - Dia 2 - Unicamp 2026

Sua conquista começa aqui!
Novidade! Correção inteligente - simulado seus resultados.
Sua conquista começa aqui!

Gabarito

  • Questão ativa

  • Já visualizadas

  • Não visualizadas

  • Resolução pendente

  • ANL

    Questão anulada

  • S/A

    Sem alternativas

Questão 5

Dissertativa
5

Na arquitetura, uma “oval” é uma figura formada por dois pares de arcos de circunferência com raios distintos. Esses arcos se conectam nos pontos de tangência entre as  circunferências.

(Adaptado de Oval. Wikipedia) 

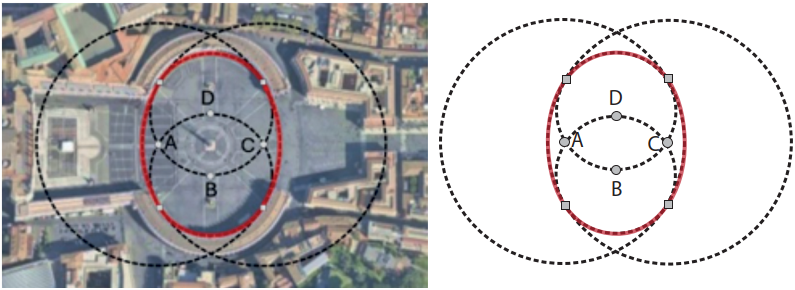
(Imagem adaptada de Google Maps. Acesso em 08/09/2025.)

A Praça de São Pedro, no Vaticano, concebida pelo renomado artista italiano Gian Lorenzo Bernini, é um exemplo notável do uso desse formato na arquitetura. As duas circunferências menores têm o mesmo raio, e o mesmo acontece com as duas circunferências maiores. Os centros das duas circunferências menores (pontos B e D) estão situados nos chamados “centro del colonnato”, distam 65 metros um do outro e o centro de uma circunferência está contido na outra circunferência, e vice-versa. 
Os centros das circunferências maiores (pontos A e C), por sua vez, estão posicionados nas interseções das circunferências menores, conforme ilustrado na imagem. Os centros das quatro circunferências formam um losango ABCD.

a) Calcule a área do losango ABCD.

b) Calcule o perímetro da oval (curva em vermelho na imagem).

Resolução:

a) 

I. Como o quadrilátero ABCD é um  losango então pode-se afirmar que ao segmentos AB, BC, CD, AD e DB possuem a mesma medida, pois todos estes segmentos são raios das duas circunferências menores, assim o tal losango é constituído de 2 triângulos equiláteros.

II. AABCD = 2 · A∆BCD = 2 · l2 34 = 2 · 652 34 = 2 112,5 3 m2

b)

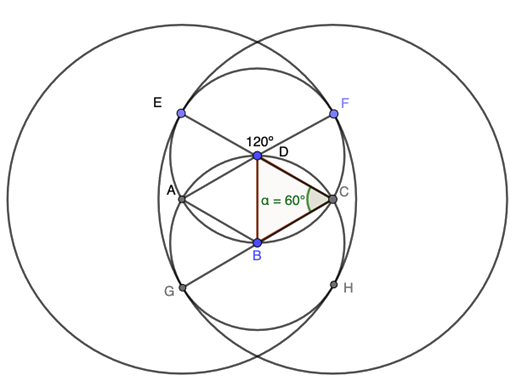
I. No desenho acima pode-se afirmar que a med (ED^F) = 120° e a med (DC^B) = 60°, assim pode-se chegar ao valor pedido através da seguinte sentença: med(EG^)  + med(FG^) + med(EF^) + med(GH^).

II. Porém EG^ ≅ FG^ ≅ e EF^ ≅ GH^, assim pode-se escrever a tal sentença 2 · medEG^ + 2 · medEF^ = 2 · 60º360º · 2πR + 2120º360º · 2πR, onde R e r são respectivamente os raios das circunferências maior e menor.

Logo; 2 · 60º360º · 2π · 130 + 2120º360º · 2π · 65=2π3 · 130+ 4.π3 · 65 =5203π m2

5

Downloads

  • Provas

Fique por dentro das novidades

Inscreva-se em nossa newsletter para receber atualizações sobre novas resoluções, dicas de estudo e informações que vão fazer a diferença na sua preparação!