Fique por dentro das novidades
Inscreva-se em nossa newsletter para receber atualizações sobre novas resoluções, dicas de estudo e informações que vão fazer a diferença na sua preparação!
Questão ativa
Já visualizadas
Não visualizadas
Resolução pendente
Questão anulada
Sem alternativas

Bend é uma técnica usada na guitarra para alterar a frequência sonora de uma nota musical. Essa técnica consiste em deslocar, na direção perpendicular ao braço da guitarra, o dedo que prende a corda, aumentando-se a tensão aplicada na corda e a frequência sonora emitida.
a) A frequência do harmônico fundamental de uma corda é dada por , sendo L o comprimento, T a tensão e a densidade linear da corda. No espaço de respostas, a figura A ilustra o bend (com o ângulo fora de escala) sendo aplicado no meio de uma corda (ponto P) de densidade linear . Na situação da figura A, com o bend aplicado, tem-se e . Qual é o módulo da força que deve ser aplicada sobre a corda no ponto P, ao longo da direção y, para manter o equilíbrio?
Dados: .
b) No espaço de respostas, a figura B mostra o braço de uma guitarra com uma corda diferente daquela do item anterior. Em cada casa do braço, estão indicadas a nota e a frequência do harmônico fundamental correspondente com a corda presa sem o bend. Nesses casos, a tensão na corda é a mesma para todas as notas, dada por . Se um bend é feito para elevar a frequência da nota Sol para a frequência da nota Sol sustenido (Sol#), qual é o aumento na tensão da corda?
Use a relação:
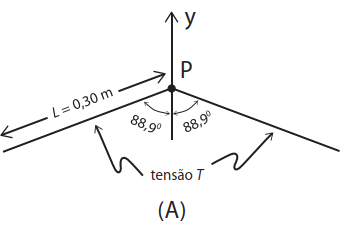

a) Dados:
Pela expressão fornecida no enunciado, tem-se:
A partir da disposição dos vetores ilustrados na figura a seguir, pode-se calcular a intensidade da força F na situação de equilíbrio da corda.
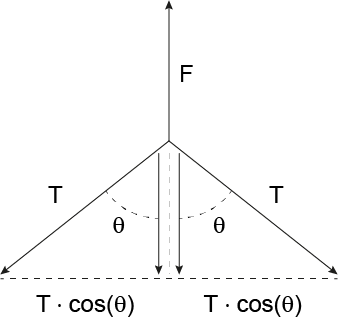
b) Dados:
Pela expressão fornecida no enunciado, tem-se:
Inscreva-se em nossa newsletter para receber atualizações sobre novas resoluções, dicas de estudo e informações que vão fazer a diferença na sua preparação!