Fique por dentro das novidades
Inscreva-se em nossa newsletter para receber atualizações sobre novas resoluções, dicas de estudo e informações que vão fazer a diferença na sua preparação!
Questão ativa
Já visualizadas
Não visualizadas
Resolução pendente
Questão anulada
Sem alternativas

Um LED (do inglês Light-Emitting Diode) é um componente eletrônico que emite luz quando sujeito a uma diferença de potencial e percorrido por uma corrente elétrica.
a) A cor de um LED monocromático depende da frequência f da luz emitida, que, de forma simplificada, é determinada pela expressão , em que é a carga do elétron e h é a constante de Planck. Calcule o valor de h considerando um LED que emite luz de comprimento de onda e que opere com .
Dado: velocidade da luz .
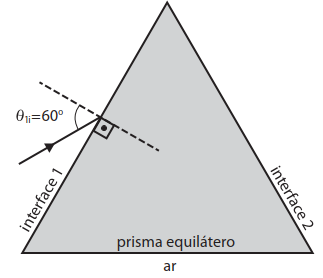
b) O índice de refração n de um meio depende do comprimento de onda da luz que o atravessa. Isso permite analisar a composição espectral da luz, como a emitida por um LED. O prisma equilátero (secção reta) do espaço de respostas, imerso em ar , foi usado para estudar um raio de luz monocromática para o qual o índice de refração do prisma é . O raio incide na interface 1 (ar–prisma), com ângulo , sendo parcialmente refletido e parcialmente refratado.
(i) Calcule o ângulo de refração na interface 1;
No prisma no espaço de respostas,
(ii) desenhe o caminho do raio dentro do prisma e depois de emergir do mesmo, na interface 2 (prisma-ar), explicitando os valores dos ângulos envolvidos;
(iii) desenhe o raio da primeira reflexão na interface 1, indicando o valor ângulo de .
a) Dados:
Pela expressão fornecida no enunciado, tem-se:
A unidade da constante de Planck pode ser determinada a partir das grandezas físicas da expressão .
Recordando que , obtém-se:
b) Dados:
i) Calculando o valor de :
Recorrendo à lei de Snell na interface 1:
ii) Desenhando o caminho do raio de luz ao atravessar o prisma, tem-se:
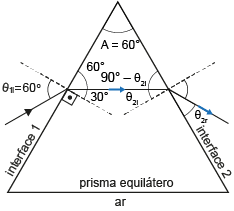
Pela figura apresentada, tem-se:
Recorrendo à lei de Snell na interface 2:
Pelos cálculos apresentados, vê-se que o raio de luz refrata na interface 1 e percorre um caminho paralelo à base do prisma, saindo dele na interface 2 com um ângulo igual ao ângulo de entrada.
iii) Obtendo o ângulo de reflexão na interface 1:
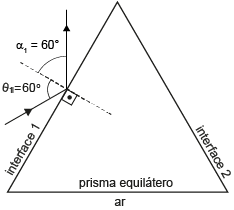
De acordo com a segunda lei da reflexão, tem-se , conforme ilustra a figura anterior.
Inscreva-se em nossa newsletter para receber atualizações sobre novas resoluções, dicas de estudo e informações que vão fazer a diferença na sua preparação!