Questão 87 - 1ª Fase - Unesp 2026

Novidade! Correção inteligente - simulado seus resultados.

Selecione uma prova

Gabarito

Geral
1. 1E
2. 2A
3. 3C
4. 4B
5. 5D
6. 6E
7. 7C
8. 8E
9. 9C
10. 10D
11. 11A
12. 12D
13. 13B
14. 14E
15. 15C
16. 16E
17. 17D
18. 18A
19. 19D
20. 20B
21. 21E
22. 22E
23. 23B
24. 24C
25. 25D
26. 26D
27. 27A
28. 28E
29. 29C
30. 30A
31. 31E
32. 32D
33. 33B
34. 34E
35. 35A
36. 36C
37. 37A
38. 38C
39. 39B
40. 40B
41. 41D
42. 42E
43. 43A
44. 44C
45. 45B
46. 46A
47. 47E
48. 48D
49. 49B
50. 50C
51. 51E
52. 52A
53. 53C
54. 54E
55. 55D
56. 56B
57. 57A
58. 58D
59. 59C
60. 60E
61. 61D
62. 62C
63. 63A
64. 64B
65. 65E
66. 66B
67. 67A
68. 68C
69. 69D
70. 70C
71. 71C
72. 72A
73. 73E
74. 74B
75. 75E
76. 76A
77. 77B
78. 78D
79. 79C
80. 80A
81. 81C
82. 82B
83. 83E
84. 84C
85. 85D
86. 86A
87. 87A
88. 88A
89. 89D
90. 90B

Questão ativa
Já visualizadas
Não visualizadas
Resolução pendente
ANL
Questão anulada
S/A
Sem alternativas

Questão 87

Objetiva

A figura indica o pentágono UNESP, formado pelo quadrado UNSP e pelo triângulo equilátero NES, que compartilham o lado $NS$ , de medida igual a 4 cm. Sabe-se, ainda, que a circunferência indicada na figura possui centro N e tangencia $SE$ no ponto T.

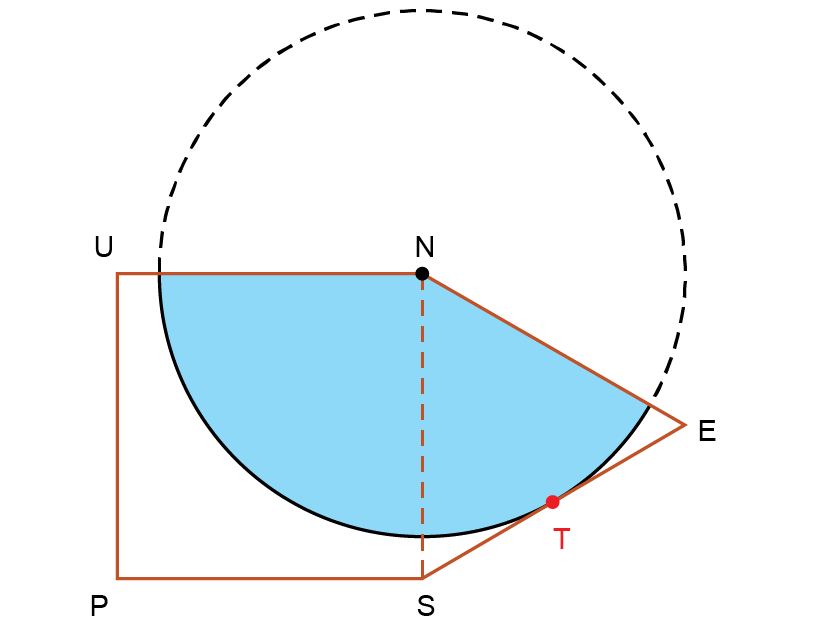
Adotando $\frac{π}{4 + \sqrt{3}} = 0, 548$ , da região do pentágono UNESP, aquela que está ocupada pelo setor circular de centro N, indicado na figura azul, corresponde a

Alternativas

A
68,5%.
B
66,5%.
C
70,5%.
D
72,5%.
E
74,5%.

Gabarito:
A

Do enunciado, sabe-se que o lado do triângulo equilátero NES mede 4 cm. Se o ponto T é o ponto de tangência, então $NT$ é a altura do triângulo equilátero e o raio da circunferência. Assim, tem-se:

$R = \frac{L \sqrt{3}}{2} = \frac{4 \sqrt{3}}{2} = 2 \sqrt{3} cm$

Calculando-se a área do pentágono UNESP, tem-se:

$A_{UNESP} = L^{2} + \frac{L^{2} \sqrt{3}}{4} = 4^{2} + \frac{4^{2} \sqrt{3}}{4} A_{UNESP} = (16 + 4 \sqrt{3}) {cm}^{2}$

Calculando a área do setor circular azul, utilizando-se como ângulo interno a soma dos ângulos internos do quadrado e do triângulo (90° + 60°), tem-se:

$A_{SETOR} = \frac{150 °}{360 °} \cdot π \cdot R^{2} = \frac{150 °}{360 °} \cdot π \cdot (2 {\sqrt{3}}^{2}) = \frac{5}{12} \cdot π \cdot 12 A_{SETOR} = 5 π {cm}^{2}$

Assim, a razão entre a área do setor e a área do pentágono é dada por:

$p = \frac{A_{SETOR}}{A_{UNESP}} = \frac{5 π}{(16 + 4 \sqrt{3})} = \frac{5 π}{4 \cdot (4 + \sqrt{3})} = \frac{5}{4} \cdot 0, 548 p = 0, 685 = 68, 5 %$

Downloads

Provas

Fique por dentro das novidades

Inscreva-se em nossa newsletter para receber atualizações sobre novas resoluções, dicas de estudo e informações que vão fazer a diferença na sua preparação!