Questão 25 - Prova Modelo A - AFA 2025

Selecione uma prova

Gabarito

Geral
1. 1B
2. 2B
3. 3C
4. 4D
5. 5D
6. 6C
7. 7C
8. 8A
9. 9D
10. 10A
11. 11ANL
12. 12D
13. 13B
14. 14B
15. 15C
16. 16A
17. 17C
18. 18C
19. 19B
20. 20D
21. 21B
22. 22A
23. 23C
24. 24A
25. 25B
26. 26D
27. 27A
28. 28A
29. 29B
30. 30B
31. 31D
32. 32D
33. 33B
34. 34D
35. 35B
36. 36A
37. 37D
38. 38C
39. 39D
40. 40C
41. 41D
42. 42A
43. 43B
44. 44B
45. 45B
46. 46D
47. 47C
48. 48A
49. 49A
50. 50C
51. 51D
52. 52D
53. 53B
54. 54A
55. 55D
56. 56B
57. 57C
58. 58A
59. 59D
60. 60C
61. 61B
62. 62A
63. 63A
64. 64B
65. REDRED
66. TXTTXT

Questão ativa
Já visualizadas
Não visualizadas
Resolução pendente
ANL
Questão anulada
S/A
Sem alternativas

Questão 25

Objetiva

Considere um triângulo retângulo cujo perímetro mede 15 unidades de comprimento e que seus lados estão em uma progressão aritmética crescente. A partir desse triângulo, podemos inscrever uma circunferência de raio 𝒓, bem como circunscrever outra circunferência de raio 𝑹. Então, a razão entre o raio da circunferência circunscrita e o raio da circunferência inscrita, nessa ordem, pertence ao intervalo:

Alternativas

A
[1, 2[
B
[2, 3[
C
[3, 4[
D
[4, 5]

Gabarito:
B

O triângulo em questão está desenhado na figura a seguir:

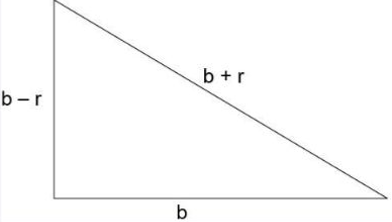
Como o perímetro é 15, tem-se:

b – r + b + b + r = 15

3b = 15

b = 5

Por Pitágoras, tem-se:

{(b - r)}^{2} + b^{2} = {(b + r)}^{2} b^{2} - 2 \cdot b \cdot r + r^{2} + b^{2} = b^{2} + 2 \cdot b \cdot r + r^{2} b^{2} = 4 \cdot b \cdot r r = \frac{b}{4} = \frac{5}{4}

Assim, o triângulo ficará:

Tem-se que o semi-perímetro é:

p = \frac{15}{2}

A área do triângulo pode ser escrita como:

A = \frac{1}{2} \cdot 5 \cdot \frac{15}{4} = \frac{75}{8}

Para o cálculo do raio da circunferência inscrita, usa-se:

A = r \cdot p \frac{75}{8} = r \cdot \frac{15}{2} r = \frac{5}{4}

Para o cálculo do raio da circunferência, usa-se:

R = \frac{a \cdot b \cdot c}{4 \cdot A} = \frac{\frac{15}{4} \cdot 5 \cdot \frac{25}{4}}{4 \cdot \frac{75}{8}} = \frac{25}{8}

Por fim:

\frac{R}{r} = \frac{\frac{25}{8}}{\frac{5}{4}} = \frac{5}{2} = 2, 5

Downloads

Provas

Fique por dentro das novidades

Inscreva-se em nossa newsletter para receber atualizações sobre novas resoluções, dicas de estudo e informações que vão fazer a diferença na sua preparação!