Questão 15 - 1ª Fase - IME 2026

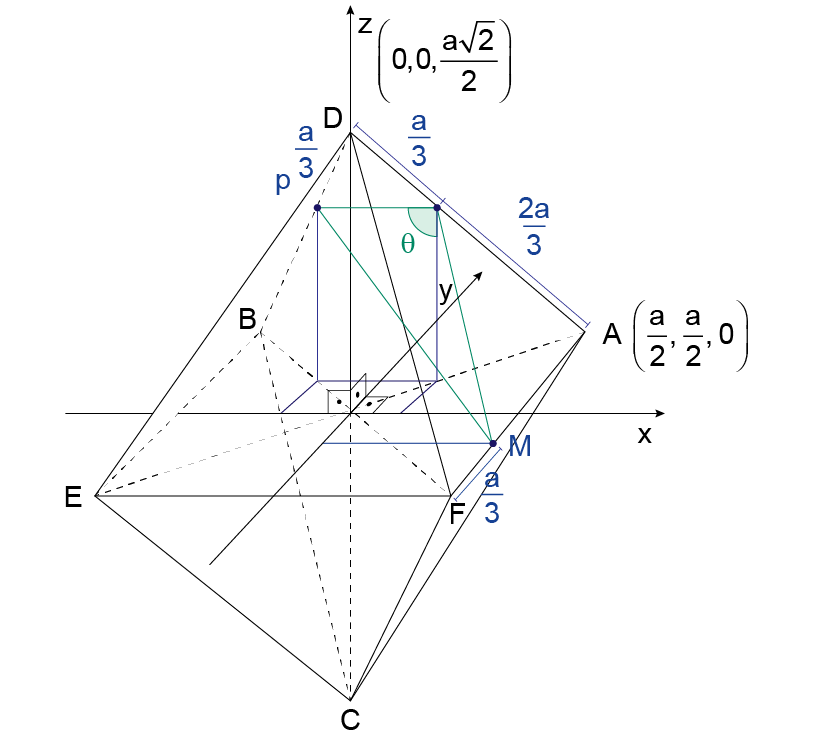
É preciso criar um sistema de coordenadas com origem no cruzamento das diagonais, eixo x paralelo ao lado AB, eixo y paralelo ao lado AF e eixo z sobre a diagonal CD. Nesse sistema, tem-se:

$$\begin{gathered} \mathrm{A}=\left(\frac{\mathrm{a}}{2};\frac{\mathrm{a}}{2};0\right), \mathrm{D}=\left(0;0;\frac{\mathrm{a}\sqrt{2}}{2}\right) \\ \mathrm{M}=\left(\frac{\mathrm{a}}{2};-\left(\frac{\mathrm{a}}{2}-\frac{\mathrm{a}}{3}\right);0\right)=\left(\frac{\mathrm{a}}{2};-\frac{\mathrm{a}}{6};0\right) \\ \mathrm{N}=\left(\frac{1}{3}·\frac{\mathrm{a}}{2};\frac{1}{3}·\frac{\mathrm{a}}{2};\frac{2}{3}·\frac{\mathrm{a}\sqrt{2}}{2}\right)=\left(\frac{\mathrm{a}}{6};\frac{\mathrm{a}}{6};\frac{\mathrm{a}\sqrt{2}}{3}\right) \\ \mathrm{P}=\left(-\frac{1}{3}·\frac{\mathrm{a}}{2};\frac{1}{3}·\frac{\mathrm{a}}{2};\frac{2}{3}·\frac{\mathrm{a}\sqrt{2}}{2}\right)=\left(-\frac{\mathrm{a}}{6};\frac{\mathrm{a}}{6};\frac{\mathrm{a}\sqrt{2}}{3}\right) \end{gathered}$$

Assim:

$\mathrm{MN}=\sqrt{{\left(\frac{\mathrm{a}}{2}-\frac{\mathrm{a}}{6}\right)}^2+{\left(-\frac{\mathrm{a}}{6}-\frac{\mathrm{a}}{6}\right)}^2+{\left(0-\frac{\mathrm{a}\sqrt{2}}{3}\right)}^2}=\sqrt{\frac{{\mathrm{a}}^2+{\mathrm{a}}^2+2{\mathrm{a}}^2}{9}}=\sqrt{\frac{4{\mathrm{a}}^2}{9}}=\frac{2\mathrm{a}}{3}$

$\mathrm{NP}=\sqrt{{\left(\frac{\mathrm{a}}{6}+\frac{\mathrm{a}}{6}\right)}^2+{\left(\frac{\mathrm{a}}{6}-\frac{\mathrm{a}}{6}\right)}^2+{\left(\frac{\mathrm{a}\sqrt{2}}{3}-\frac{\mathrm{a}\sqrt{2}}{3}\right)}^2}=\sqrt{\frac{{\mathrm{a}}^2}{9}}=\frac{\mathrm{a}}{3}$

$\mathrm{MP}=\sqrt{{\left(\frac{\mathrm{a}}{2}+\frac{\mathrm{a}}{6}\right)}^2+{\left(-\frac{\mathrm{a}}{6}-\frac{\mathrm{a}}{6}\right)}^2+{\left(0-\frac{\mathrm{a}\sqrt{2}}{3}\right)}^2}=\sqrt{\frac{4{\mathrm{a}}^2+{\mathrm{a}}^2+2{\mathrm{a}}^2}{9}}=\sqrt{\frac{7{\mathrm{a}}^2}{9}}=\frac{\mathrm{a}\sqrt{7}}{3}$

Sendo $\mathrm{\theta }=\mathrm{M}\hat{\mathrm{N}}\mathrm{P}$, aplica-se a lei dos cossenos no triângulo MNP:

$\mathrm{cos\theta }=\frac{{\mathrm{MN}}^2+{\mathrm{NP}}^2-{\mathrm{MP}}^2}{2·\mathrm{MN}·\mathrm{NP}}=\frac{{\left({\displaystyle \frac{2\mathrm{a}}{3}}\right)}^2+{\left({\displaystyle \frac{\mathrm{a}}{3}}\right)}^2-{\left({\displaystyle \frac{\mathrm{a}\sqrt{7}}{3}}\right)}^2}{2·{\displaystyle \frac{2\mathrm{a}}{3}}·{\displaystyle \frac{\mathrm{a}}{3}}}=\frac{{\displaystyle \frac{-2{\mathrm{a}}^2}{9}}}{{\displaystyle \frac{4{\mathrm{a}}^2}{9}}}=-\frac{1}{2}$

Logo, $\boxed{\mathrm{\theta }=\frac{2\mathrm{\pi }}{3}}$.