Questão 13 - 1ª Fase - IME 2026

a: semieixo real 

b: semieixo imaginário 

c: semidistância focal

Na hipérbole:

$\frac{{\mathrm{x}}^2}{16}-\frac{{\mathrm{y}}^2}{9}=1$

Tem-se: $\mathrm{a}=4, \mathrm{b}=3 \mathrm{e} \mathrm{c}=\sqrt{{\mathrm{a}}^2+{\mathrm{b}}^2}=5.$

O centro da hipérbole é $\left(0; 0\right)$, e os focos são $\mathrm{F}=\left(5; 0\right) \mathrm{e} \mathrm{F}\text{'}=\left(-5; 0\right).$

A equação da assíntota de coeficiente angular positivo é dada por:

$\mathrm{s}: \mathrm{y}=\frac{\mathrm{b}}{\mathrm{a}}\mathrm{x}\to \mathrm{y}=\frac{3}{4}\mathrm{x}$

Observe a figura:

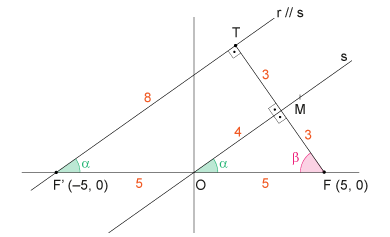
A tangente de $\mathrm{\alpha }$ é o coeficiente angular de s, ou seja, é igual a $\frac{3}{4}$. Assim, o triângulo $\mathrm{OMF}$ é um $\left(3, 4, 5\right)$. Traçando por T uma reta $\mathrm{r} \left|\right| \mathrm{s}$, observa-se que onde ela cruzar o eixo x, formará, com F e T, um triângulo $\left(6, 8, 10\right)$. Como $\mathrm{FF}\text{'}=2\mathrm{c}=10,$ a reta r cruzará o eixo x em $\mathrm{F}\text{'}$. Logo, o triângulo $\mathrm{FF}\text{'}\mathrm{T}$ é $\left(6, 8, 10\right)$ e o raio da circunferência inscrita é dado por:

$\mathrm{r}=\frac{[\mathrm{FF}\text{'}\mathrm{T}]}{\mathrm{p}}=\frac{{\displaystyle \frac{6·8}{2}}}{{\displaystyle \frac{6+8+10}{2}}}=\frac{24}{12}=\boxed{2}$