Fique por dentro das novidades
Inscreva-se em nossa newsletter para receber atualizações sobre novas resoluções, dicas de estudo e informações que vão fazer a diferença na sua preparação!

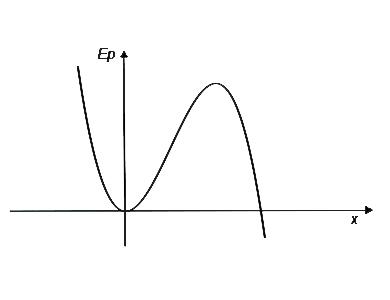
A figura mostra o aspecto da curva da energia potencial de uma partícula em movimento unidimensional, cuja equação é dada por
,
sendo a força associada aplicada à particula dada por
.
Observação:
Dado o exposto:
a) determine o intervalo de posições possíveis para a partícula para que seu movimento seja oscilatório;
b) determine o supremo da energia mecânica abaixo do qual a partícula possa conservar-se em movimento oscilatório;
c) esboce o gráfico da velocidade em função do tempo se, num instante inicial, em , o sentido da velocidade da partícula é da direita para a esquerda e sua energia mecânica é tal que .
a) Para que ocorra movimento oscilatório é preciso inicialmente de um equilíbrio estável:
Porém, é preciso verificar se ambos se tratam de equilíbrios estáveis, por enquanto sabe-se apenas que são pontos de equilíbrio. Para isso, sendo um ponto de equilíbrio e o pequeno deslocamento em relação ao equilíbrio, é necessário que para que a força seja restauradora.
Para :
Como :
para todo pequeno Estável.
Para :
Como :
para todo pequeno Instável.
Portanto, só tem-se equilíbrio estável, o que permite movimento oscilatório, em torno de . Como em tem-se equilíbrio instável, caso a partícula tenha energia para chegar até , não haverá força restauradora, então .
Porém, caso a partícula esteja em com energia potencial suficiente para chegar em , também deixará de oscilar ao passar de .
Apesar de ser uma equação do terceiro grau, sabe-se que é raiz (dupla, por sinal).
Então, em tem-se a mesma energia que em . Pelo gráfico do enunciado, se , a energia potencial aumenta. Ou seja, só há movimento oscilatório se:
Observação: também é possível pensar qualitativamente desde o início que, para que exista um movimento oscilatório, a partícula precisa estar “presa” em um poço de potencial, o que ocorre entre e .
b) A existência de uma máxima energia potencial foi discutida no item a) e vale:
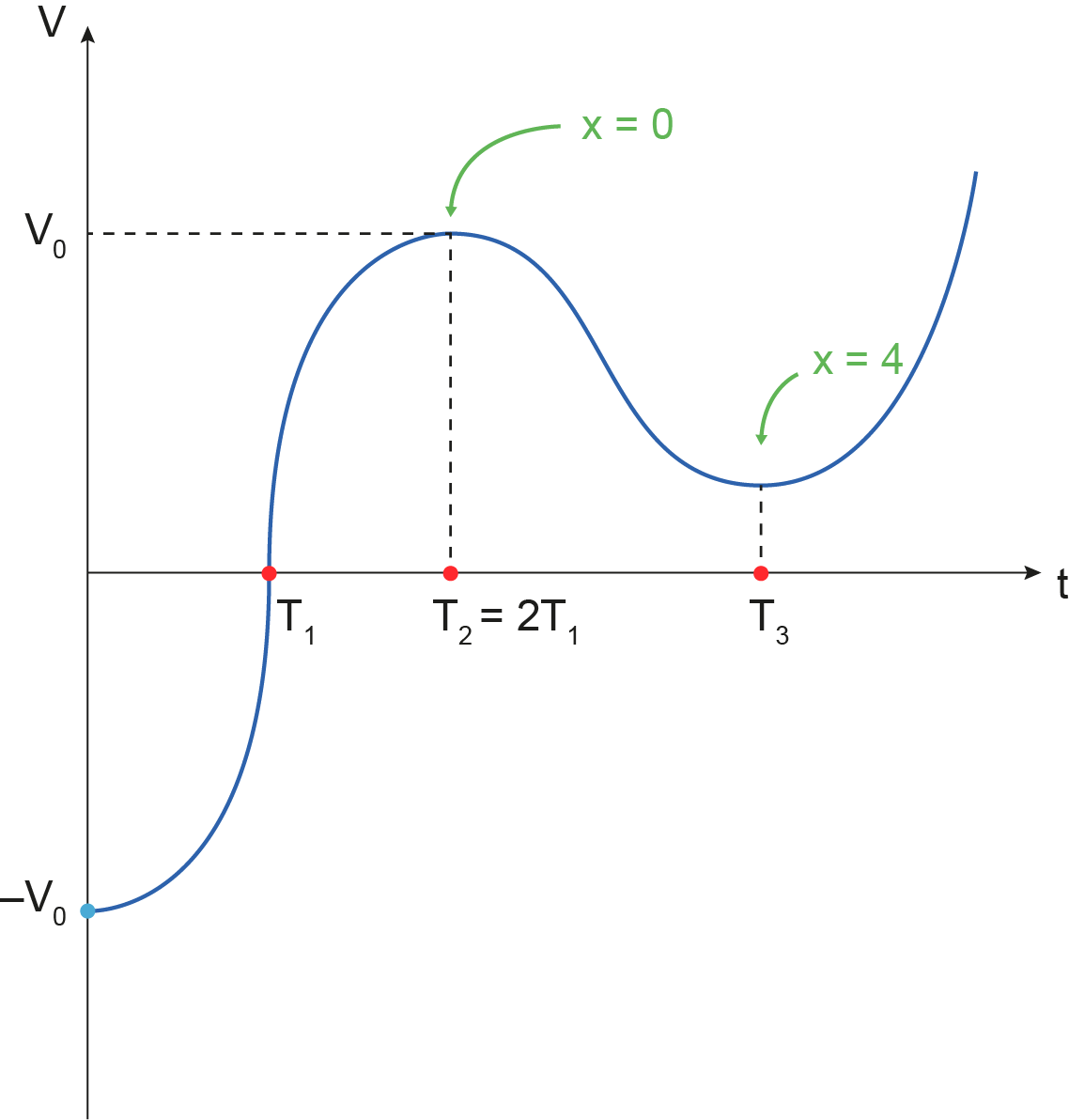
c)
Segue então o esboço do gráfico:
Inscreva-se em nossa newsletter para receber atualizações sobre novas resoluções, dicas de estudo e informações que vão fazer a diferença na sua preparação!