Dissertativa 10 - 2ª Fase - Dia 2 - IME 2026

Clique aqui e veja a resolução ITA 1ª Fase 2026

Novidade! Correção inteligente - simulado seus resultados.

Selecione uma prova

Gabarito

Física
1. 1DIS
2. 2DIS
3. 3DIS
4. 4DIS
5. 5DIS
6. 6DIS
7. 7DIS
8. 8DIS
9. 9DIS
10. 10DIS

Questão ativa
Já visualizadas
Não visualizadas
Resolução pendente
ANL
Questão anulada
S/A
Sem alternativas

Questão 10

Dissertativa

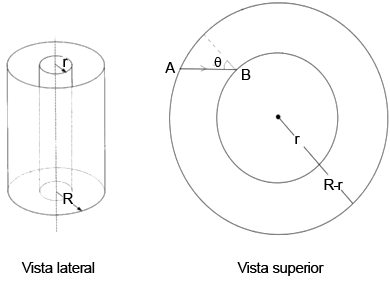
Sejam dois cilindros coaxiais de raios $R$ e $r$ , com $R > r$ . O cilindro de raio $R$ tem sua superfície interna espelhada, enquanto a superfície externa do cilindro de raio $r$ também é espelhada.

Um feixe estreito de luz se propaga entre os espelhos em um plano perpendicular ao eixo dos cilindros. O feixe luminoso parte do ponto A, é refletido no ponto B e, a partir daí, continua sua trajetória entre os espelhos.

Considerando que o sistema esteja ajustado à razão $r / R = \sqrt{3} / 2$ para que haja $n$ pontos de reflexão em cada espelho, onde $n \in ℕ$ , e que os raios se sobrepõem após uma volta, calcule:

a) a expressão de $\tan θ$ em função de $n$ .
b) os valores possíveis de $n$ .

Resolução:

a) A figura a seguir ilustra a trajetória seguida pelo raio de luz:

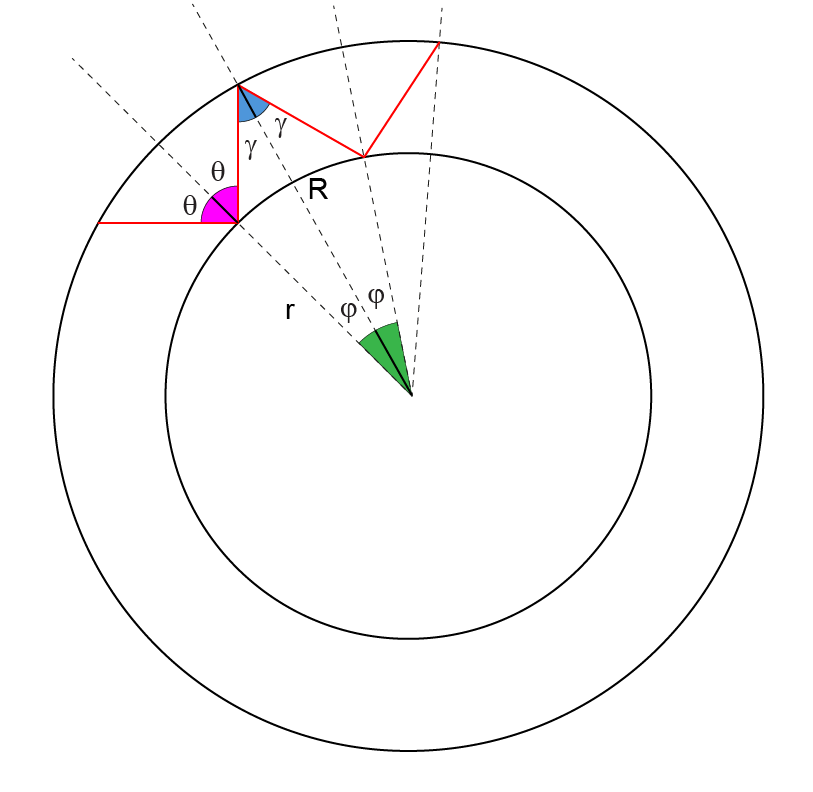
Condição para o raio voltar ao ponto inicial:

$n \cdot R \cdot 2 φ = 2 πR \Rightarrow φ = \frac{π}{n}$

Lei dos senos:

$\frac{sen (180 ° - θ)}{R} = \frac{senγ}{r} \Rightarrow \frac{senθ}{R} = \frac{sen (θ - φ)}{r} \Rightarrow \frac{sen (θ - φ)}{senθ} = \frac{r}{R}$

$\frac{senθ \cdot cosφ - senφ \cdot cosθ}{senθ} = \frac{\sqrt{3}}{2} \Rightarrow 2 senθ \cdot cosφ - 2 senφ \cdot cosθ = \sqrt{3} senθ$

$2 tgθ \cdot cosφ - 2 senφ = \sqrt{3} tgθ \Rightarrow tgθ = \frac{2 senφ}{2 cosφ - \sqrt{3}}$

$tgθ = \frac{2 sen (π / n)}{2 \cos (π / n) - \sqrt{3}}$

b) Como $0 < θ < π / 2$ :

$tgθ > 0 \Rightarrow 2 \cos (\frac{π}{n}) - \sqrt{3} > 0 \Rightarrow \cos (\frac{π}{n}) > \frac{\sqrt{3}}{2} \Rightarrow \frac{π}{n} < \frac{π}{6} \Rightarrow n > 6$

Downloads

Provas

Fique por dentro das novidades

Inscreva-se em nossa newsletter para receber atualizações sobre novas resoluções, dicas de estudo e informações que vão fazer a diferença na sua preparação!