Dissertativa 4 - 2ª Fase - Dia 2 - IME 2026

Novidade! Correção inteligente - simulado seus resultados.

Clique aqui e veja a resolução ITA 1ª Fase 2026

Selecione uma prova

Gabarito

Física
1. 1DIS
2. 2DIS
3. 3DIS
4. 4DIS
5. 5DIS
6. 6DIS
7. 7DIS
8. 8DIS
9. 9DIS
10. 10DIS

Questão ativa
Já visualizadas
Não visualizadas
Resolução pendente
ANL
Questão anulada
S/A
Sem alternativas

Questão 4

Dissertativa

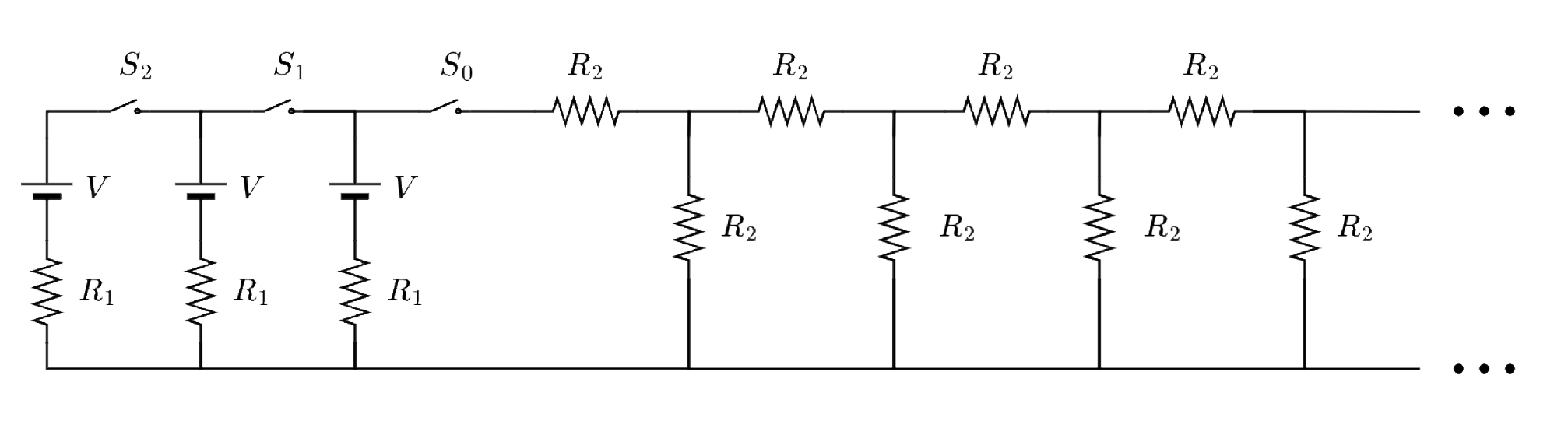
Considere o circuito da figura composto por três fontes iguais, três resistências de valor $R_{1}$ , três chaves e uma malha infinita de resistências de valor $R_{2}$ . Sabe-se que a chave $S_{0}$ é fechada em $t = 0$ , a chave $S_{1}$ é fechada em $t = 20 s$ , a chave $S_{2}$ é fechada em $t = 40 s$ e que nenhuma das chaves muda seu estado após o fechamento.

Dados:

$V = 40 V$ ;
$R_{1} = 6 Ω$ ;
$R_{2} = (\sqrt{5} - 1) Ω$ .

Dado o exposto, calcule o valor da energia total dissipada na malha infinita de resistências entre os instantes $t = 0$ e $t = 60 s$ .

Resolução:

Tomando a resistência equivalente dos resistores a seguir como $R$ :

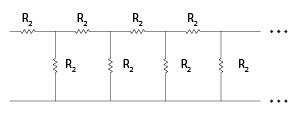
Tem-se:

Assim:

$R = (R_{2} / / R) + R_{2} R = \frac{R_{2} R}{R_{2} + R} + R_{2} \to (R - R_{2}) (R + R_{2}) = R_{2} R R^{2} - R_{2}^{2} = R_{2} R \to R^{2} - R_{2} R - R_{2}^{2} = 0 R = \frac{R_{2} \pm \sqrt{R_{2}^{2} + 4 R_{2}^{2}}}{2}$

Como $R > 0$ :

$R = R_{2} \frac{(1 + \sqrt{5})}{2}$

Com o valor do enunciado:

$R = \frac{(\sqrt{5} - 1) (\sqrt{5} + 1)}{2} \to R = 2 Ω$

No intervalo $0 \leq t < 20 s :$

Com um gerador de $40 V$ e resistência interna $6 Ω$ :

$i = \frac{40}{6 + 2} \to i = 5 A P = i^{2} R = 5^{2} \cdot 2 \to P = 50 W E_{1} = (50 W) (20 s) = 1000 J$

No intervalo $20 s \leq t < 40 s :$

Com dois geradores de $40 V$ e resistência interna $6 Ω$ em paralelo, tem-se um gerador equivalente de $40 V$ e $3 Ω$ :

$i = \frac{40}{3 + 2} \to i = 8 A P = i^{2} R = 8^{2} \cdot 2 \to P = 128 W E_{1} = (128 W) (20 s) = 2560 J$

No intervalo $40 s \leq t \leq 60 s :$

Com três geradores de $40 V$ e resistência interna $6 Ω$ em paralelo, tem-se um gerador equivalente de $40 V$ e $2 Ω$ :

$i = \frac{40}{2 + 2} \to i = 10 A P = i^{2} R = 10^{2} \cdot 2 \to P = 200 W E_{1} = (200 W) (20 s) = 4000 J$

Portanto, a energia total dissipada é de:

$E = 1000 + 2560 + 4000 E = 7560 J$

Downloads

Provas

Fique por dentro das novidades

Inscreva-se em nossa newsletter para receber atualizações sobre novas resoluções, dicas de estudo e informações que vão fazer a diferença na sua preparação!