Dissertativa 3 - 2ª Fase - Dia 2 - IME 2026

Clique aqui e veja a resolução ITA 1ª Fase 2026

Novidade! Correção inteligente - simulado seus resultados.

Selecione uma prova

Gabarito

Física
1. 1DIS
2. 2DIS
3. 3DIS
4. 4DIS
5. 5DIS
6. 6DIS
7. 7DIS
8. 8DIS
9. 9DIS
10. 10DIS

Questão ativa
Já visualizadas
Não visualizadas
Resolução pendente
ANL
Questão anulada
S/A
Sem alternativas

Questão 3

Dissertativa

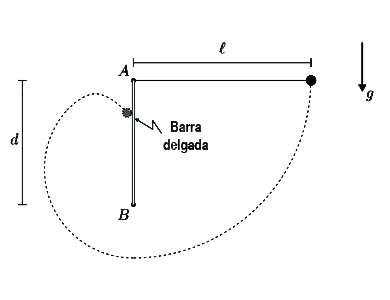
Uma pequena esfera é presa ao ponto $A$ indicado na figura por um fio de comprimento $ℓ$ . Abaixo e na mesma vertical de $A$ , a uma distância $d$ , há o ponto $B$ , de forma que uma barra delgada imóvel é fixada entre $A$ e $B$ .

Em um determinado momento, a esfera é posicionada à direita de $A$ , de maneira que o fio esteja esticado na horizontal. Na sequência, a esfera é solta, passando a movimentar-se em uma trajetória que descreve um quarto de circunferência em torno de $A$ e, ao passar por baixo do ponto $B$ , parte do fio encosta e gruda na barra e a esfera continua seu movimento.

Dado:

aceleração da gravidade: $g$ .

Observação:

o fio é inextensível e de massa desprezível.

Determine, em função de $ℓ$ e de acordo com o contexto apresentado:

a) o valor mínimo de $d$ para que a trajetória descrita pela esfera após passar por baixo de $B$ seja uma semicircunferência;

b) o raio de curvatura instantâneo, caso $d = 3 / 7 l$ , da trajetória da esfera em seu ponto mais alto após ter passado por baixo do ponto $B$ .

Resolução:

a) O valor mínimo de d é aquele no qual a bolinha chega no ponto mais alto da trajetória com tração nula.

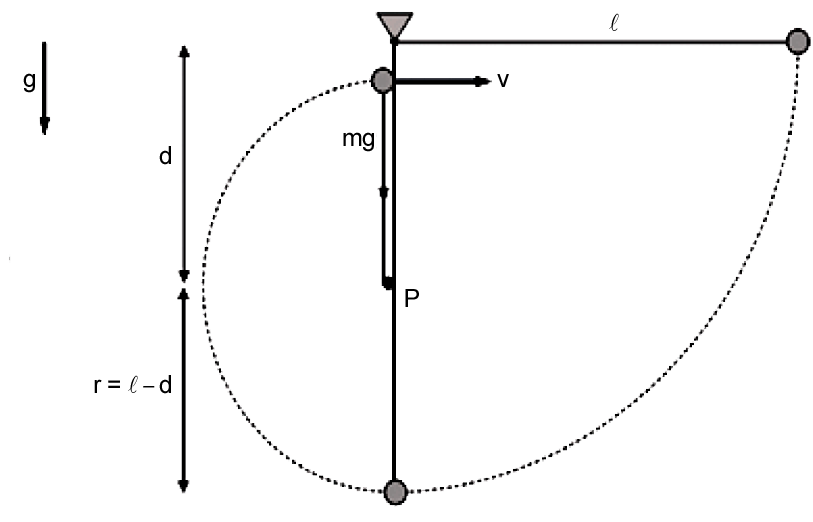
Pela conservação de energia:

$E_{{mec}_{i}} = E_{{mec}_{f}} \Rightarrow mg l = mg \cdot 2 r + \frac{{mv}^{2}}{2} \Rightarrow 2 g l = 4 g \cdot (l - d) + v^{2} \Rightarrow v^{2} = 2 g (2 d - l)$

No ponto mais alto:

$R_{cp} = mg = \frac{{mv}^{2}}{r} \Rightarrow v^{2} = gr \Rightarrow v^{2} = g (l - d)$

Igualando as duas equações acima:

$2 g (2 d - l) = g (l - d) \Rightarrow d = \frac{3 l}{5}$

b) Nesta nova condição, o fio se afrouxa antes de atingir o ponto mais alto.

$r = l - d = l - \frac{3 l}{7} \Rightarrow r = \frac{4 l}{7}$

A figura a seguir ilustra o momento em que o fio se afrouxa:

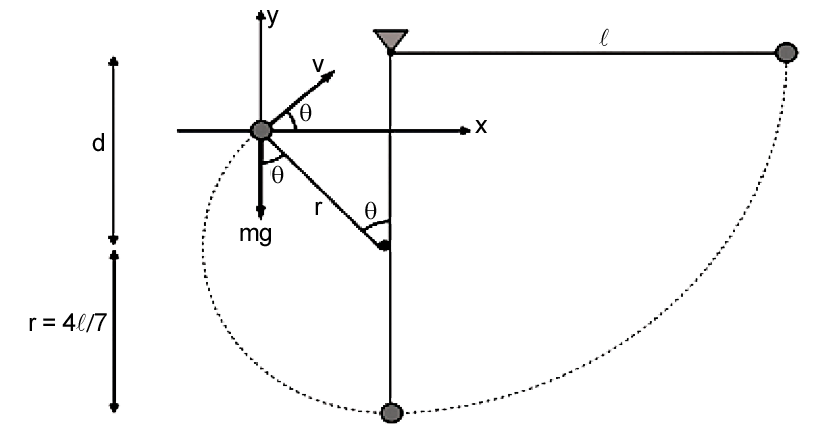
Pela conservação de energia:

$E_{{mec}_{i}} = E_{{mec}_{f}} \Rightarrow mg l = mg \cdot r (1 + cosθ) + \frac{{mv}^{2}}{2} \Rightarrow 2 g l = 2 g \cdot \frac{4 l}{7} \cdot (1 + cosθ) + v^{2} v^{2} = \frac{2 g l}{7} (3 - 4 cosθ)$

No ponto em que o fio se afrouxa:

$R_{cp} = mgcosθ = \frac{{mv}^{2}}{r} \Rightarrow v^{2} = \frac{4 g l}{7} \cdot cosθ$

Igualando as duas equações acima:

$\frac{2 g l}{7} (3 - 4 cosθ) = \frac{4 g l}{7} cosθ \Rightarrow cosθ = \frac{1}{2}$

Logo:

$v^{2} = \frac{4 g l}{7} \cdot \frac{1}{2} \Rightarrow v^{2} = \frac{2 g l}{7}$

A partir do momento em que o fio se afrouxa, a esfera realiza um lançamento oblíquo e, no ponto mais alto, o raio de curvatura instantâneo $ρ$ é tal que:

$R_{cp} = mg = \frac{m {(vcosθ)}^{2}}{ρ} \Rightarrow g \cdot ρ = v^{2} \cdot \cos^{2} θ \Rightarrow g \cdot ρ = \frac{2 g l}{7} \cdot \frac{1}{4} \Rightarrow ρ = \frac{l}{14}$

Downloads

Provas

Fique por dentro das novidades

Inscreva-se em nossa newsletter para receber atualizações sobre novas resoluções, dicas de estudo e informações que vão fazer a diferença na sua preparação!