Dissertativa 5 - 2ª Fase - Dia 2 - IME 2026

Novidade! Correção inteligente - simulado seus resultados.

Clique aqui e veja a resolução ITA 1ª Fase 2026

Selecione uma prova

Gabarito

Física
1. 1DIS
2. 2DIS
3. 3DIS
4. 4DIS
5. 5DIS
6. 6DIS
7. 7DIS
8. 8DIS
9. 9DIS
10. 10DIS

Questão ativa
Já visualizadas
Não visualizadas
Resolução pendente
ANL
Questão anulada
S/A
Sem alternativas

Questão 5

Dissertativa

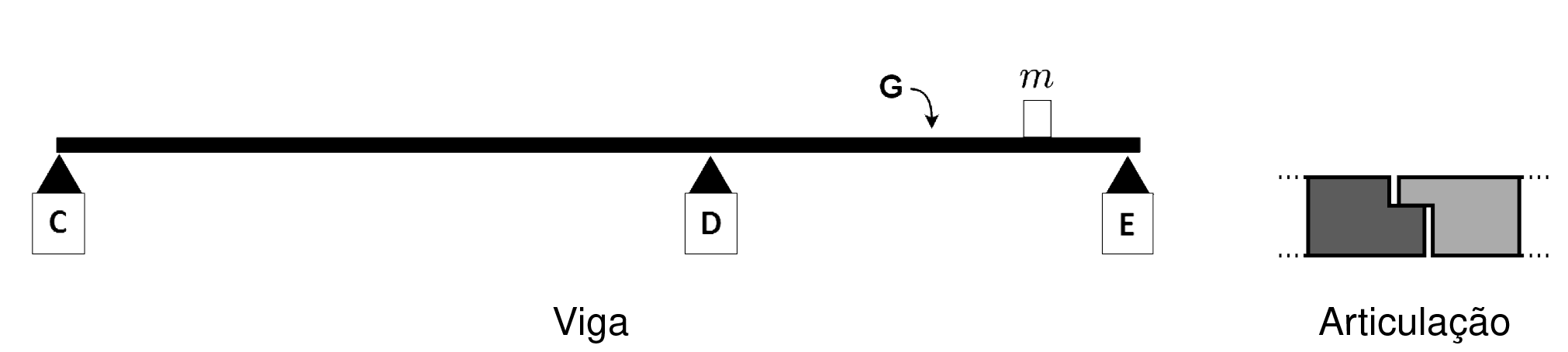
Uma viga homogênea de comprimento total L e massa M está apoiada horizontalmente em três apoios verticais simples indicados na figura por C, D e E. No trecho DE, repousa um bloco de massa m. No ponto G, localizado também no trecho DE, é instalada uma articulação que interrompe a continuidade estrutural da viga.

Dados:

comprimento da viga: L = 10 m;
massa da viga: M = 6 kg;
distâncias entre os apoios: CD = 6 m e DE = 4 m;
distância entre a articulação e o apoio E: GE = 2 m;
distância entre o bloco de massa m e o apoio E: 1 m;
aceleração da gravidade: $g = 10 m / s^{2}$ .

Observações:

a viga é considerada indeformável em todas as suas partes;
após a instalação da articulação, a seção da viga entre os pontos G e E passa a ser apoiada em dois pontos: o dente da articulação em G e o apoio E.

Mediante o contexto, determine:

a) as reações de apoio em C, D, E e G para m = 4 kg;

b) o maior valor de m de forma que a articulação consiga manter a viga em equilíbrio.

Resolução:

A barra tem densidade linear de massa $λ = 0, 6 kg / m$ . Além disso, o enunciado deixa claro que o apoio G é tal que as forças trocadas entre os trechos CD e DE são puramente verticais. Isolando-se esses trechos, vem:

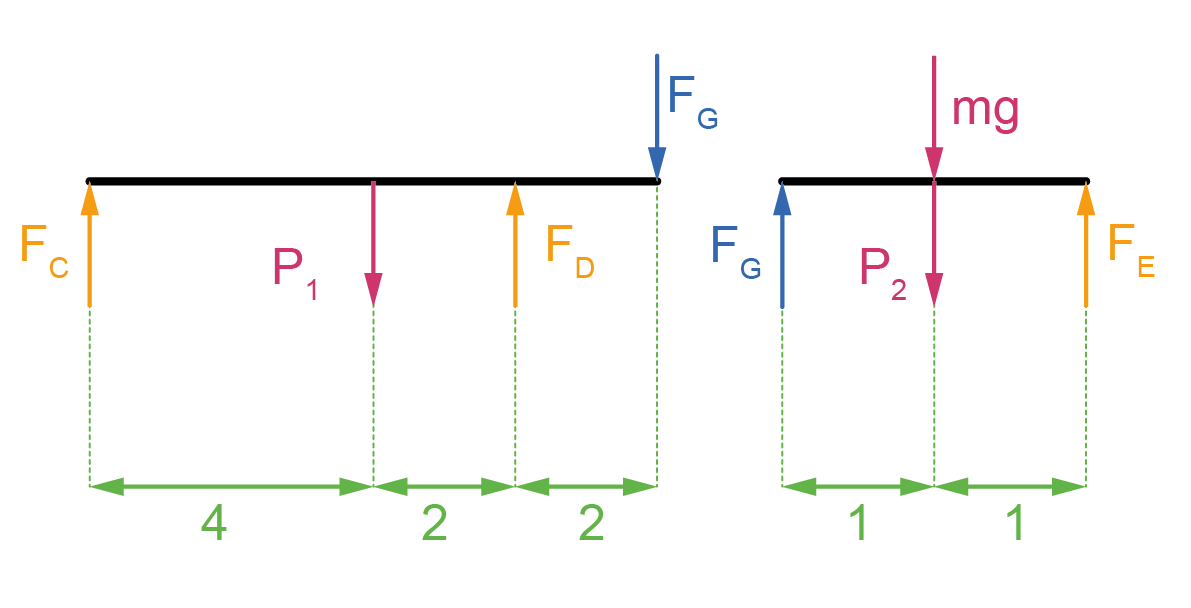
Em que:

$P_{1} = 0, 6 \cdot 8 \cdot 10 = 48 N$
$P_{2} = 0, 6 \cdot 2 \cdot 10 = 12 N$

a) Se m = 4 kg, então mg = 40 N.

Equilíbrio de torques sobre GE em relação a E:

$P_{2} \cdot 1 + mg \cdot 1 = F_{G} \cdot 2 \Rightarrow 12 + 40 = 2 F_{G} \Rightarrow F_{G} = 26 N$

Equilíbrio translacional de GE:

$F_{G} + F_{E} = P_{2} + mg \Rightarrow 26 + F_{E} = 12 + 40 \Rightarrow F_{E} = 26 N$

Equilíbrio rotacional de CG em relação a C:

$P_{1} \cdot 4 + F_{G} \cdot 8 = F_{D} \cdot 6 \Rightarrow 48 \cdot 4 + 26 \cdot 8 = 6 F_{D} \Rightarrow 400 = 6 F_{D} \Rightarrow F_{D} = \frac{200}{3} N$

Equilíbrio translacional de CG:

$F_{C} + F_{D} = P_{1} + F_{G} \Rightarrow F_{C} + \frac{200}{3} = 48 + 26 \Rightarrow F_{C} = \frac{22}{3} N$

b) Se a massa m for suficientemente grande, a força $F_{G}$ pode fazer a barra CG tombar para a direita. Quando isso ocorrer, todo o contato estará concentrado no ponto D $(logo F_{C} = 0)$ . Nota-se que a barra GE não apresenta risco de tombar devido ao posicionamento simétrico das cargas.

Equilíbrio rotacional da barra CG, em relação a D, na iminência de tombar:

$P_{1} \cdot 2 = F_{G} \cdot 2 \Rightarrow F_{G} = P_{1} \Rightarrow F_{G} = 48 N$

Equilíbrio rotacional de GE em relação a E:

$F_{G} \cdot 2 = (P_{2} + mg) \cdot 1 \Rightarrow 96 = 12 + 10 m \Rightarrow m = 8, 4 kg$

Downloads

Provas

Fique por dentro das novidades

Inscreva-se em nossa newsletter para receber atualizações sobre novas resoluções, dicas de estudo e informações que vão fazer a diferença na sua preparação!