Questão 48 - 1ª Fase - Einstein 2026

O número de ligações entre cada minuto pode ser representado por uma progressão aritmética de razão 3 e primeiro termo 4 (4, 7, 10, ...). O total do número de ligações é dado pela soma dessa PA, cuja fórmula é ${\mathrm{S}}_{\mathrm{n}} = \frac{({\mathrm{a}}_1 + {\mathrm{a}}_{\mathrm{n}}) · \mathrm{n}}{2}$, em que:

$$\begin{gathered} {\mathrm{a}}_1 = 4 \\ {\mathrm{a}}_{\mathrm{n}} = {\mathrm{a}}_1 + (\mathrm{n} - 1) · \mathrm{r} = 4 + (\mathrm{n} - 1) · 3 = 4 + 3\mathrm{n} - 3 = 3\mathrm{n} + 1 \end{gathered}$$

É desejável que essa soma seja maior que 1 000. Logo: 

$$\begin{gathered} \frac{(4 + 3\mathrm{n} + 1) · \mathrm{n}}{2} > 1 000 \\ (3\mathrm{n} + 5) · \mathrm{n} > 2 000 \\ 3{\mathrm{n}}^2 + 5\mathrm{n} > 2 000 \\ 3{\mathrm{n}}^2 + 5\mathrm{n} - 2 000 > 0 \end{gathered}$$

Utilizando a fórmula de Bhaskara, obtêm-se as raízes dessa função, que são $\frac{-80}{3}$ e 25, e identifica-se a forma do gráfico, mostrada a seguir:

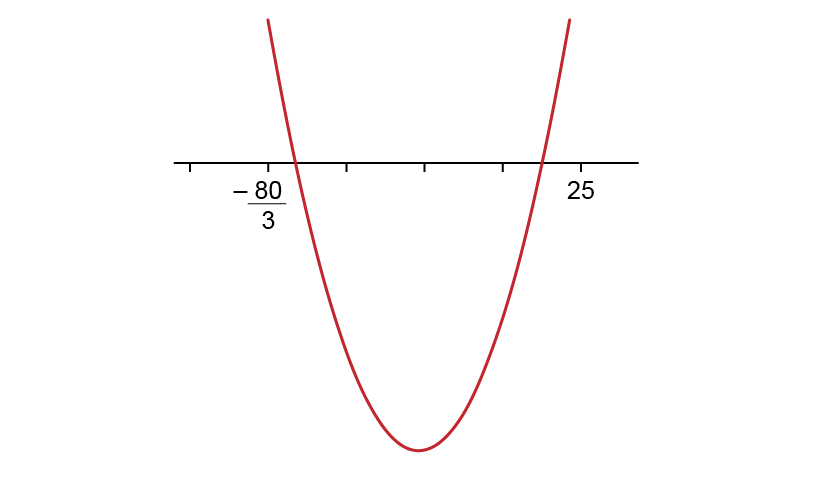
Como se considera a função maior que 0 e n, um número positivo, conclui-se que n > 25. Portanto, o número de telefonemas passará de 1 000 após 0h25, ou seja, entre 0h25 e 0h26.