Fique por dentro das novidades
Inscreva-se em nossa newsletter para receber atualizações sobre novas resoluções, dicas de estudo e informações que vão fazer a diferença na sua preparação!

Um cilindro foi colocado no interior de um cubo cuja aresta mede 4 cm, de tal maneira que cada base do cilindro tangencia três faces do cubo, conforme mostra a figura 1. Cada um desses 6 pontos de tangência está a uma distância d de duas das arestas da face que o contém, conforme a figura 2, que mostra detalhadamente uma das bases do cilindro.
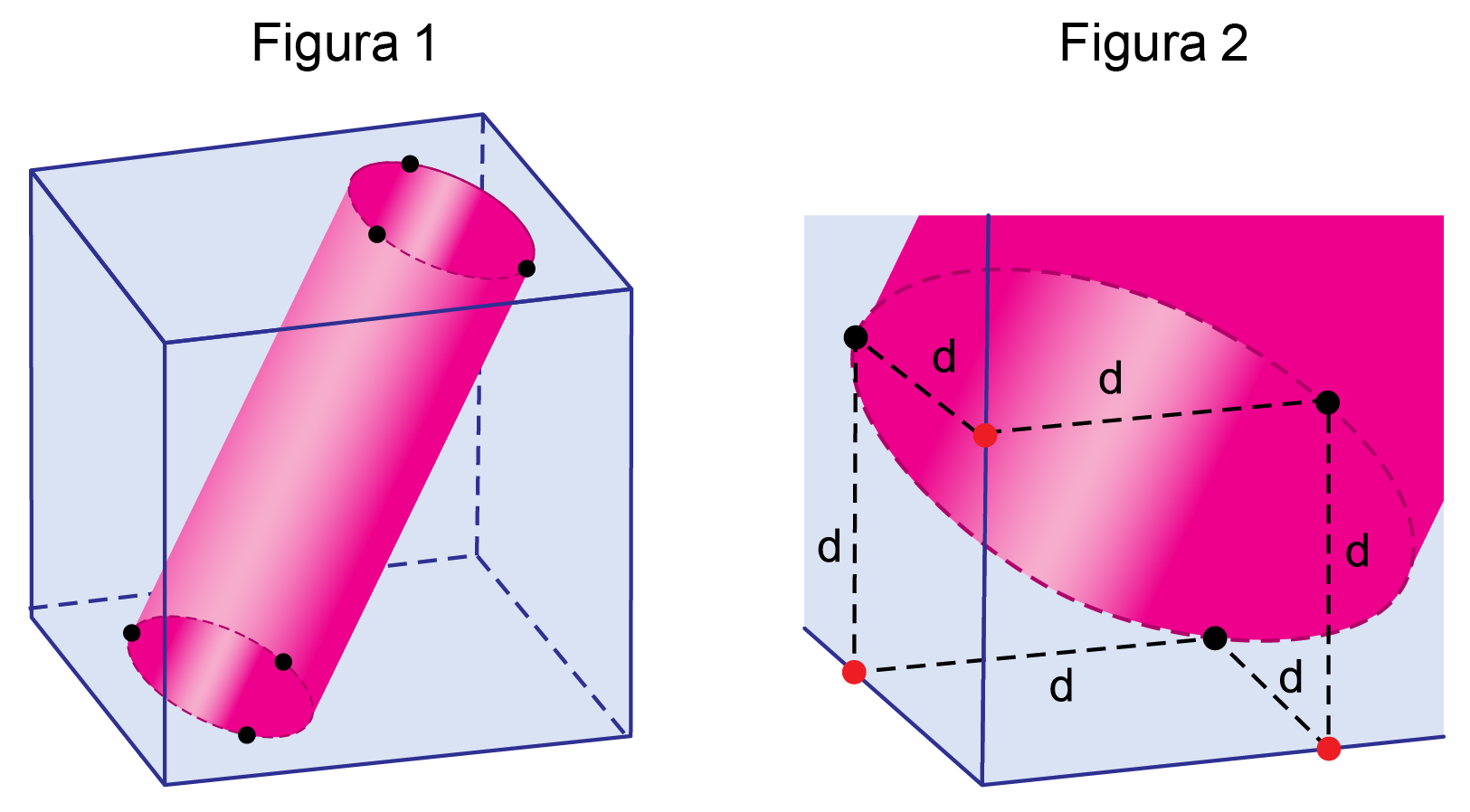
a) Supondo que cm, qual é a área do triângulo cujos vértices são os três pontos de tangência de uma mesma base do cilindro?
b) Se d = 1 cm, o raio da base do cilindro medirá cm. Nessas condições, qual o volume do cilindro?
a) O triângulo formado pelos pontos de tangência é equilátero, e cada lado mede:
Sabendo que , tem-se:
A área de um triângulo equilátero de lado a é dada por:
Substituindo a = 2:
b) Na figura 2, considera-se x a distância do vértice do cubo até o centro da base do cilindro. Forma-se um triângulo retângulo entre o vértice do cubo, o centro da base do cilindro e um ponto de tangência.
Pelo teorema de Pitágoras:
Sabendo que o raio do cilindro é a distância do centro da base até o ponto de tangência e que vale:
Logo, substituindo r e no teorema de Pitágoras:
Calculando o volume do cilindro:
A altura h é a distância entre os centros das bases do cilindro, que pode ser escrita como:
Substituindo
Inscreva-se em nossa newsletter para receber atualizações sobre novas resoluções, dicas de estudo e informações que vão fazer a diferença na sua preparação!