Fique por dentro das novidades
Inscreva-se em nossa newsletter para receber atualizações sobre novas resoluções, dicas de estudo e informações que vão fazer a diferença na sua preparação!
Dissertativas 8 - 2ª Fase - Dia 2 - Unicamp 2025
Gabarito
Biológicas
Exatas
Humanas
Questão ativa
Já visualizadas
Não visualizadas
Resolução pendente
- ANL
Questão anulada
- S/A
Sem alternativas
__c3bd2c4a-79fe-4858-a8dd-5427347f5aab.jpg)
Seja Q um quadrado de lado medindo 21 cm.
a) Considere que Q foi subdividido em 9 quadrados , cujos lados medem 7 cm. Quantos triângulos distintos podem ser formados de modo que seus vértices sejam os centros dos quadrados dessa subdivisão? Lembre-se de que dois triângulos são distintos quando seus vértices não coincidem.
b) É possível escolhermos 10 pontos em Q de modo que a distância entre quaisquer dois desses pontos seja maior do que 10 centímetros? Justifique.
Resolução:
a. Representando o enunciado em questão, tem-se o seguinte quadrado:
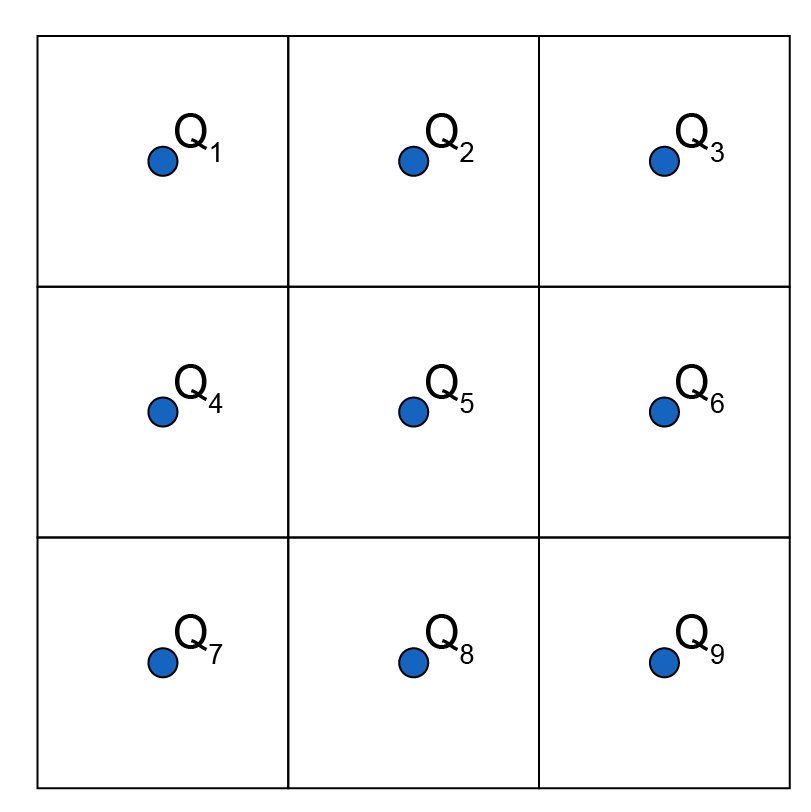
Sabe-se que, para formar um triângulo, é preciso escolher 3 pontos entre os 9. Além disso, esses 3 pontos não podem ser colineares.
Para determinar o número de triângulos formados com os 9 pontos, que sejam todos distintos, é necessário escolher sempre conjuntos diferentes de 3 pontos, além de eliminar casos de pontos colineares. Portanto, tem-se uma combinação:
Analisando as imagens a seguir, notam-se 8 casos nos quais 3 pontos são colineares.
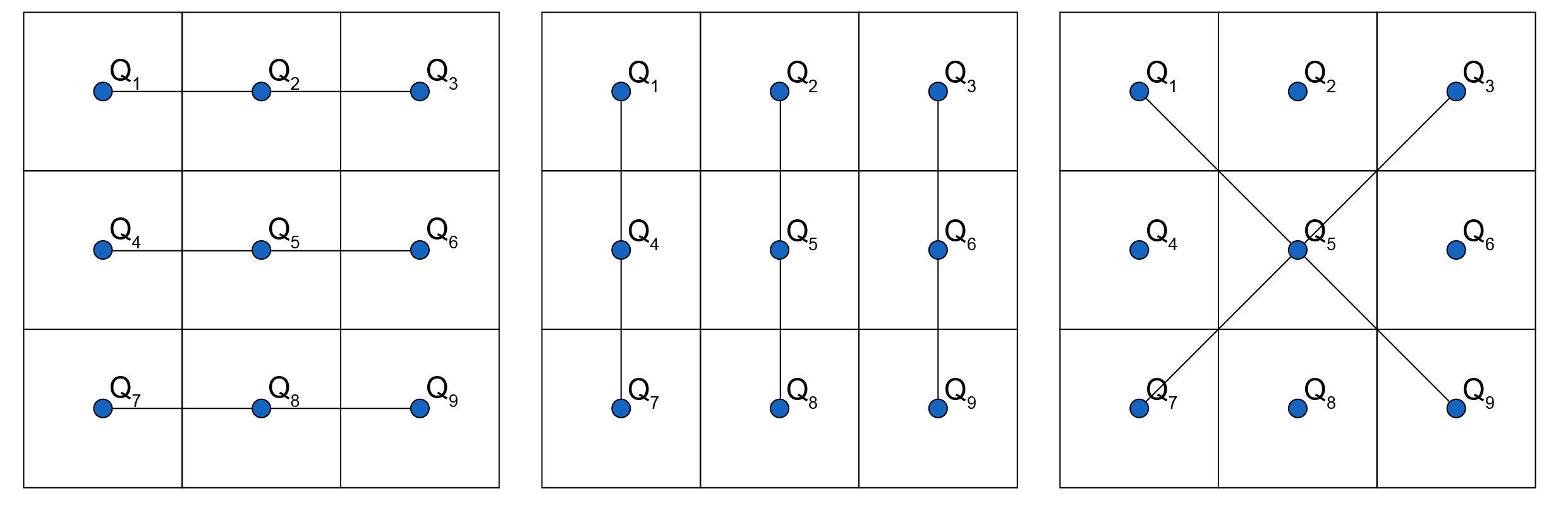
Assim, a quantidade de triângulos (3 pontos não colineares) diferentes que podem ser formados é 84 – 8 = 76.
b. A maior distância entre dois pontos pertencentes ao quadrado Q é dada pelos pontos nas extremidades de uma mesma diagonal. Ao calcular essa distância, obtém-se:
Nota-se que a maior distância possível entre dois pontos neste quadrado, , é menor do que 10. Portanto, é impossível escolher 10 pontos no quadrado Q de modo que a distância entre quaisquer dois desses pontos seja maior que 10 cm.