unicamp

Dissertativas 3 - 2ª Fase - Dia 2 - Unicamp 2025

Poliedro Curso - Turmas 2025
Poliedro Resolve - Resolução - Unicamp 1ª Fase 2025

Gabarito

  • Questão ativa

  • Já visualizadas

  • Não visualizadas

  • Resolução pendente

  • ANL

    Questão anulada

  • S/A

    Sem alternativas

Questão 3

Dissertativa
3

Rayssa participou dos Jogos Olímpicos de Paris. Ela visitou quatro pontos turísticos da cidade: o Arco do Triunfo, a Catedral de Notre-Dame, o Museu do Louvre e a Torre Eiffel.

a) Rayssa escolheu a melhor foto que tirou de cada um desses pontos turísticos e publicará uma por dia em suas redes sociais, ao longo de quatro dias consecutivos, sem repetir nenhuma foto. De quantas maneiras ela pode fazer isso? Justifique.

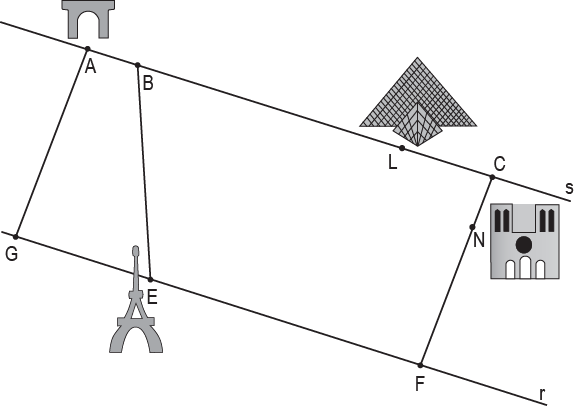
b) Na figura abaixo, o Arco do Triunfo, a Catedral de Notre-Dame, o Museu do Louvre e a Torre Eiffel estão indicados pelos pontos A, N, L e E, respectivamente. Os segmentos de reta na figura representam ruas de Paris. As retas r, s são paralelas e os segmentos de reta AG e CF são paralelos entre si e perpendiculares a r e s. 
Considere as distâncias AB = CN = 0,5, BL = 2,5, LC = 1, EF = 2,7 e BE = 1,7, dadas em quilômetros. Rayssa visitou os pontos turísticos na seguinte ordem: Arco do Triunfo, Torre Eiffel, Catedral de Notre-Dame e Museu do Louvre, percorrendo a menor distância possível, nas ruas indicadas na figura. Qual foi a distância que ela percorreu? Justifique.

Resolução:

a) Rayssa deve tirar quatro fotos diferentes e postá-las durante quatro dias consecutivos, sem repetição. Pelo princípio fundamental da contagem, o número de maneiras de se fazer isso é dado por:

4⏟1º dia·3⏟2º dia·2⏟3º dia·1⏟4º dia= 24 maneiras

b) Pelo texto, Rayssa passará pelos vértices ABEFCL. Sendo assim, calculam-se as distâncias:

  • AB = 0,5 km (dado pelo texto)
  • BE = 1,7 km (dado pelo texto)
  • EF = 2,7 km (dado pelo texto)

Pela descrição do texto, o quadrilátero AGFC é um retângulo; com isso, pelo teorema de Pitágoras, obtém-se:

FC2+0,82=1,72→FC=1,5 km

  •  CL = 1 km (dado pelo texto)

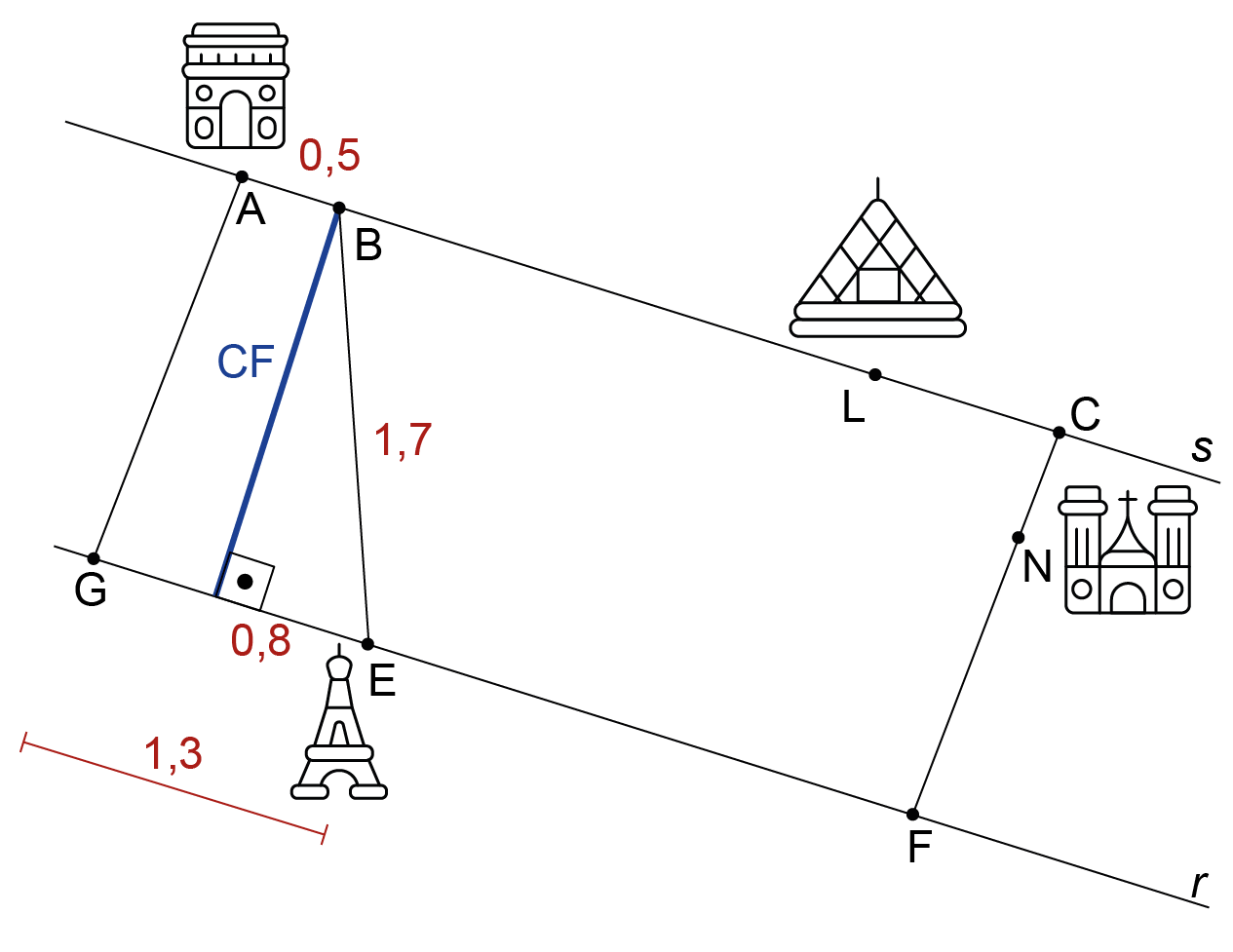
Portanto, a distância percorrida por ela foi:

AB + BE + EF + FC + CL = 0,5 + 1,7 + 2,7 + 1,5  + 1 = 7,4 km

3

Fique por dentro das novidades

Inscreva-se em nossa newsletter para receber atualizações sobre novas resoluções, dicas de estudo e informações que vão fazer a diferença na sua preparação!