Fique por dentro das novidades
Inscreva-se em nossa newsletter para receber atualizações sobre novas resoluções, dicas de estudo e informações que vão fazer a diferença na sua preparação!
Questão ativa
Já visualizadas
Não visualizadas
Resolução pendente
Questão anulada
Sem alternativas
__03d4666d-b26b-4280-8c00-0aab3fc2e35e.jpg)
Nas Olimpíadas de 2024, os atletas foram avaliados – com o emprego de metodologias modernas e conceitos de Física – em diferentes modalidades esportivas, para análise dos movimentos e diagnose de desempenho.
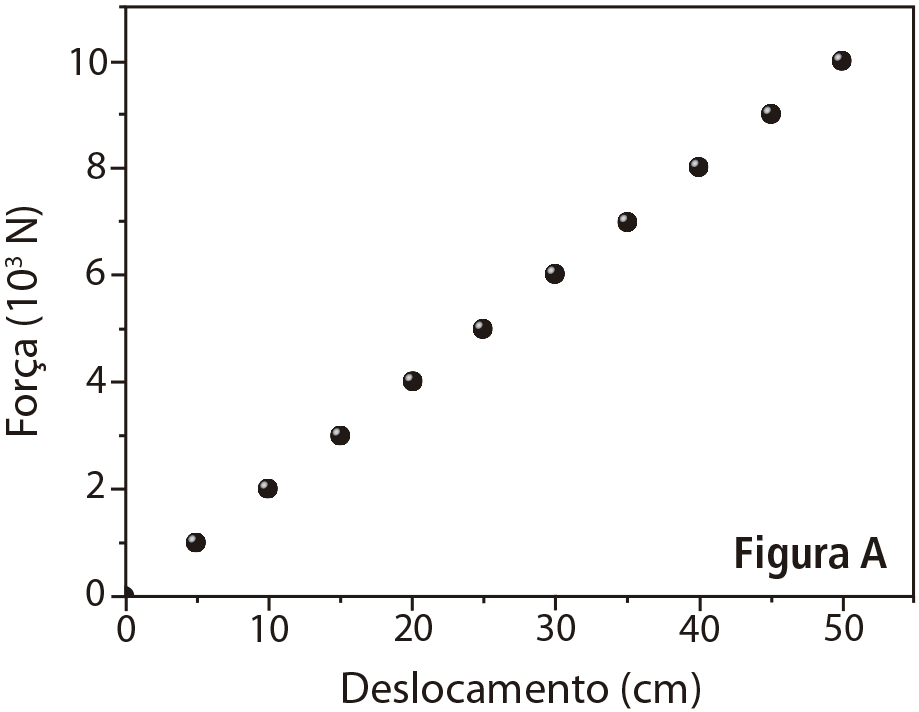
a) Nos saltos ornamentais, os atletas saltam da ponta da prancha, causando uma flexão que os impulsiona para cima. A Figura A ilustra a relação entre a força aplicada pelos atletas e o deslocamento gerado na prancha, a qual atua como uma mola sobre o atleta. Considere uma perda por atrito de 10% na energia potencial elástica. Qual a altura vertical máxima que um atleta de massa m = 72 kg atinge ao flexionar a prancha de modo a deslocar sua ponta de uma distância ∆x = 40 cm em relação à sua posição de repouso?
b) Câmeras em diferentes posições facilitam a análise dos movimentos e trajetórias nas diferentes modalidades esportivas. Algumas câmeras usam polarizadores para facilitar a visualização do objeto em movimento, com a redução de reflexões vindas das vizinhanças. A função dos polarizadores é otimizada quando essas reflexões indesejadas ocorrem na condição em que o raio refletido e o raio refratado formam um ângulo de 90°. Neste caso, o ângulo de incidência é conhecido como ângulo de Brewster . A Figura B, no espaço de respostas, mostra um raio que incide na interface entre o ar e um meio de índice de refração . O ângulo de incidência do raio é . Calcule o índice de refração .
Dados:
a. Como houve perda de 10% da Energia Mecânica durante o salto, tem-se:
, em que a energia mecânica inicial será potencial elástica, e a energia mecânica final será potencial gravitacional.
em que o K será calculado pelos dados da figura A:
Portanto, tem-se:
b.
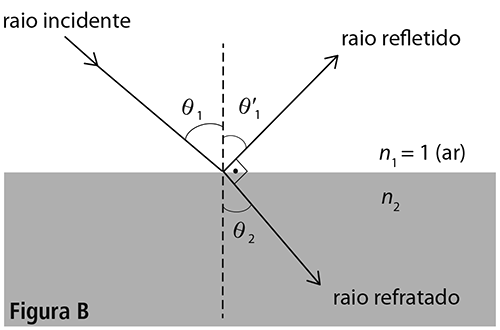
Se pela primeira lei da reflexão, tem-se . Assim:
Utilizando a lei de Snell–Descartes, tem-se:
Inscreva-se em nossa newsletter para receber atualizações sobre novas resoluções, dicas de estudo e informações que vão fazer a diferença na sua preparação!