Fique por dentro das novidades
Inscreva-se em nossa newsletter para receber atualizações sobre novas resoluções, dicas de estudo e informações que vão fazer a diferença na sua preparação!
Questão ativa
Já visualizadas
Não visualizadas
Resolução pendente
Questão anulada
Sem alternativas
__ac581119-02e8-431f-9be3-dbb610dd0c76.jpg)
Vários dispositivos eletrônicos (mouses, joysticks etc.) fazem uso do Efeito Hall. A Figura A mostra o esquema de um fluxômetro empregado para medir a vazão Z de um líquido (volume que atravessa a seção reta da tubulação por unidade de tempo) que usa esse princípio: o escoamento do líquido na tubulação gira uma turbina junto com um ímã, o que gera uma diferença de potencial () numa fita condutora.
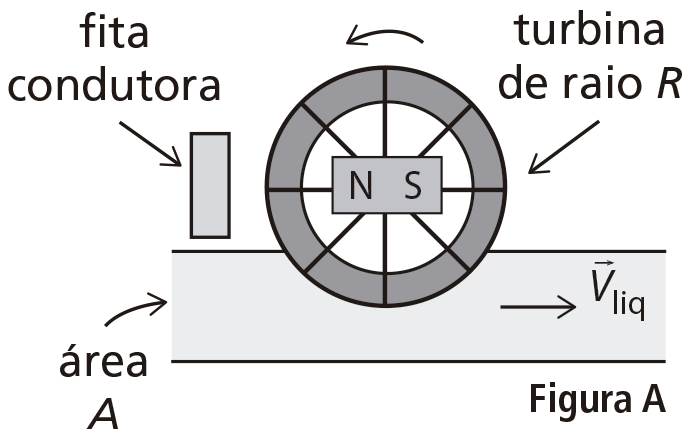
a) Com a rotação do ímã do fluxômetro, a diferença de potencial varia conforme ilustrado na Figura B no espaço de respostas, sendo máxima quando o polo norte do ímã aponta para a fita. Sendo A = 70 cm² a área da seção reta da tubulação e R = 3,0 cm o raio externo da turbina, calcule a vazão Z do líquido. Assuma que a velocidade do líquido, , seja constante e uniforme e de módulo igual ao da velocidade da extremidade da turbina.
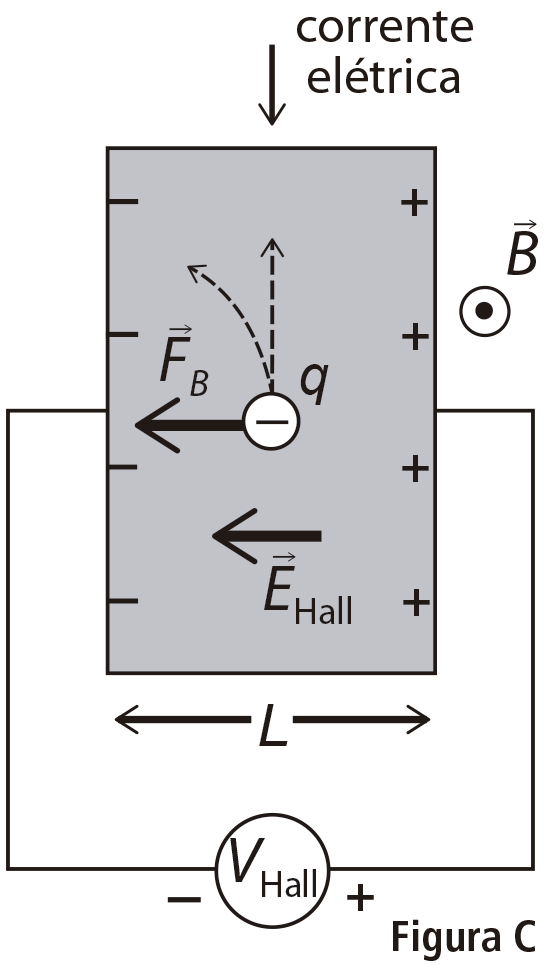
b) A Figura C mostra uma fita de largura L = 3,0 mm conduzindo corrente elétrica na presença do campo magnético que sai do papel. A força magnética desvia as cargas elétricas () responsáveis pela corrente, acumulando-as nas bordas da fita. Isso dá origem à diferença de potencial , ao campo elétrico e a uma força elétrica oposta a . Quase instantaneamente o equilíbrio de forças se estabelece e as cargas passam a seguir em linha reta, cessando o acúmulo nas bordas da fita. Para a condição de equilíbrio em que , quanto vale ?
A figura a seguir foi apresentada no espaço do caderno de prova usado para a resolução: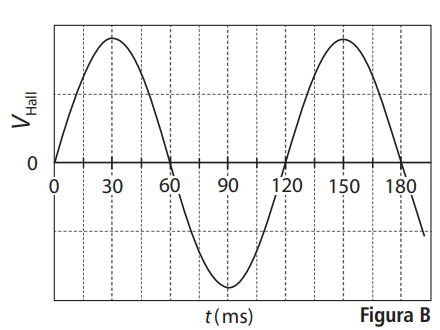
a) A vazão é dada por: Z = , em que é o volume que atravessa uma seção do fio em um intervalo de tempo .
Em uma rotação completa, o deslocamento escalar de um ponto da extremidade da turbina é dado por: . Esse deslocamento equivale ao deslocamento do líquido.
Em uma rotação completa, o volume de água é dado por:
O intervalo de tempo transcorrido é dado pela figura B, em que um ciclo completo é executado em 120 ms.
Portanto, a vazão é dada por:
b) Para que as cargas não sejam desviadas, tem-se:
em que o campo elétrico é calculado por: já que a fita se comporta como um capacitor de placas planas e paralelas.
Inscreva-se em nossa newsletter para receber atualizações sobre novas resoluções, dicas de estudo e informações que vão fazer a diferença na sua preparação!