Dissertativas 4 - 2ª Fase - Dia 2 - Unicamp 2025

a) Inicialmente, deve-se determinar g(1) e f(1):

$$\begin{gathered} \mathrm{g}\left(1\right)=1+\mathrm{K}; \\ \mathrm{f}\left(1\right)= 1^2+1+\mathrm{c}\Rightarrow \mathrm{f}\left(1\right) = 2+\mathrm{c}. \end{gathered}$$

Calculando as funções compostas f(g(1)) e g(f(1)), obtêm-se:

$$\begin{gathered} \mathrm{f}\left(\mathrm{g}\right(1\left)\right) = (\mathrm{g}{\left(1\right))}^2 + \mathrm{g}(1) + \mathrm{c} \Rightarrow \mathrm{f}(\mathrm{g}\left(1\right)) = {\mathrm{k}}^2 + 3\mathrm{k} + 2 + \mathrm{c}; \\ \mathrm{g}(\mathrm{f}\left(1\right)) = \mathrm{f}(1) + \mathrm{k} \Rightarrow \mathrm{g}(\mathrm{f}\left(1\right)) = 2 + \mathrm{c} + \mathrm{k}. \end{gathered}$$

Pela desigualdade do enunciado:

$\mathrm{f}\left(\mathrm{g}\right(1\left)\right) - \mathrm{g}\left(\mathrm{f}\right(1\left)\right) < 0 \iff {\mathrm{k}}^2 + 3\mathrm{k} + 2 + \mathrm{c} - 2 - \mathrm{c} - \mathrm{k} < 0 \iff {\mathrm{k}}^2 + 2\mathrm{k} <0.$

Ao representar o gráfico de ${\mathrm{k}}^2 + 2\mathrm{k}$, tem-se:

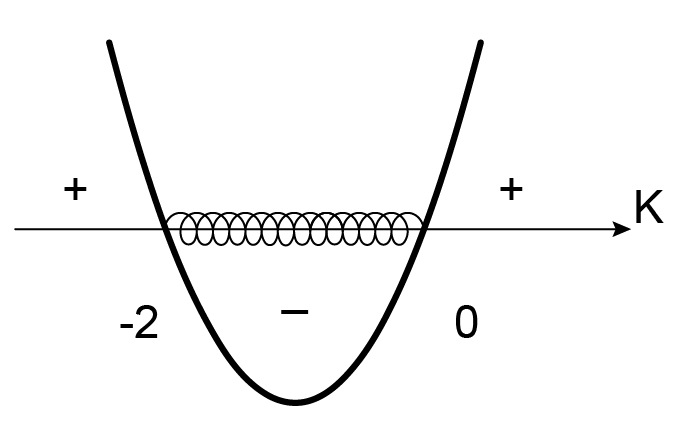
Como ${\mathrm{k}}^2 + 2\mathrm{k} < 0$, tem-se, então, $-2 < \mathrm{k} <0$.

Repare que não existem restrições para c, uma vez que ele é cancelado durante as contas, podendo, assim, assumir qualquer valor real. Portanto, $\boxed{-2 < \mathrm{k} < 0, \forall \mathrm{c}}$.

b) Como f(x) = 0 tem uma única solução, o discriminante $(∆)$ da equação ${\mathrm{x}}^2 + \mathrm{x} + \mathrm{c} = 0$ deve ser 0.

Assim, $∆ = {\mathrm{b}}^2 - 4\mathrm{ac} = 0 \iff 1^2 - 4 · 1 · \mathrm{c} = 0\iff \mathrm{c} = \frac{1}{4}$.

Como g(1) = x + k, tem-se como função inversa: ${\mathrm{g}}^{-1}\left(\mathrm{x}\right) = \mathrm{x} - \mathrm{k}$.

Dado que $\mathrm{f}\left({\mathrm{g}}^{-1}\right(\mathrm{x}\left)\right) = \frac{1}{4}$, tem-se:

$\mathrm{f}\left({\mathrm{g}}^{-1}\left(\mathrm{x}\right)\right)={\left({\mathrm{g}}^{-1}\left(\mathrm{x}\right)\right)}^2+{\mathrm{g}}^{-1}\left(\mathrm{x}\right)+\frac{1}{4}=\frac{1}{4}\iff {\left(\mathrm{x}-\mathrm{k}\right)}^2+\mathrm{x}-\mathrm{k}=0\iff {\mathrm{x}}^2+\left(-2\mathrm{k}+1\right)\mathrm{x}+{\mathrm{k}}^2-\mathrm{k}=0$.

Considere ${\mathrm{x}}_1 \mathrm{e} {\mathrm{x}}_2$ raízes da equação $\mathrm{f}\left({\mathrm{g}}^{-1}\right(\mathrm{x}\left)\right) = \frac{1}{4}$.

Pela relação de Girard, que diz respeito à soma das raízes, tem-se ${\mathrm{x}}_1 + {\mathrm{x}}_2 = -\frac{\mathrm{b}}{\mathrm{a}}$ e, pelo enunciado, a soma das raízes dessa equação é 2025. Então, ${\mathrm{x}}_1 + {\mathrm{x}}_2 = 2025 = -\frac{\mathrm{b}}{\mathrm{a}}$.

Por fim, $2025=-\frac{\left(-2\mathrm{k}+1\right)}{1}\iff \boxed{\mathrm{k}=1 013}$.