Questão 21 - 1ª Fase - ITA 2025

Considere um tanque cúbico metálico de lado $\mathrm{L}+\mathrm{a} (\mathrm{L}\gg \mathrm{a})$, aberto no topo, preenchido com água e óleo. O tanque contém, no seu interior, um cubo metálico de lado L, com 5 de seus lados totalmente submersos e o outro emerso na superfície, centralizado com a face aberta do tanque. Uma diferença de potencial de V é estabelecida entre o cubo e o tanque, de forma que o sistema atue como um capacitor. A vista frontal do sistema encontra-se ilustrada na figura. Sabe-se que o óleo possui uma densidade de${\mathrm{d}}_{\mathrm{o}}=0,90\mathrm{g}/{\mathrm{cm}}^3$ e constante dielétrica ${\mathrm{K}}_{\mathrm{o}}$, que a água tem uma densidade igual a${\mathrm{d}}_{\mathrm{a}}=1,0\mathrm{g}/{\mathrm{cm}}^3$ e constante dielétrica ${\mathrm{k}}_{\mathrm{a}}$ e que a densidade do cubo é ${\mathrm{d}}_{\mathrm{c}}=0,92\mathrm{g}/{\mathrm{cm}}^3$.

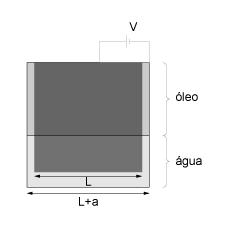
Desconsiderando efeitos de borda, assinale a alternativa que fornece a capacitância do sistema.