Fique por dentro das novidades
Inscreva-se em nossa newsletter para receber atualizações sobre novas resoluções, dicas de estudo e informações que vão fazer a diferença na sua preparação!

A figura mostra o quadrado PQRS sobre um ladrilhamento hexagonal regular do plano, em que os vértices P e Q coincidem com vértices de hexágonos do ladrilhamento.
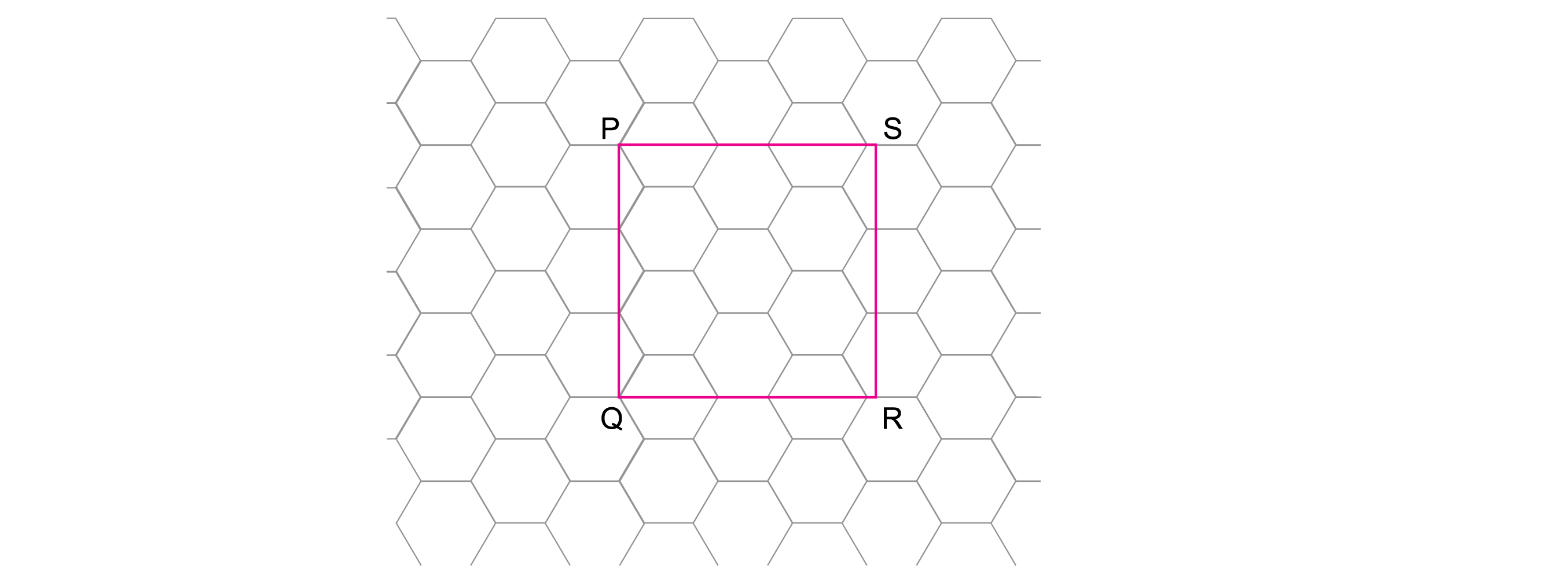
Sabendo que cada um dos hexágonos do ladrilhamento tem de área, a área do quadrado PQRS é
Pela figura, para se descobrir a medida do lado do quadrado PQRS, basta encontrar a medida da diagonal PT de um hexágono e, depois,multiplicar por 3, já que PT = TU = UQ, conforme a figura a seguir:
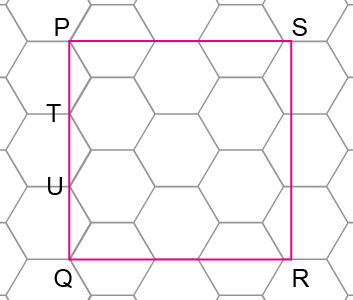
Como os hexágonos são regulares, todos os seus ângulos internos têm a mesma medida .
A soma dos ângulos internos de um hexágono é . Assim, cada ângulo interno tem medida .
Um hexágono regular de lado de medida é dividido em 6 triângulos equiláteros cujas medidas dos lados também é .

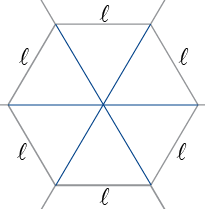
Como a área de cada triângulo equilátero é dada por , a área do hexágono é .
Como cada hexágono tem área igual a 1, conclui-se que:
Pela lei dos cossenos, sabe-se que:
Logo, a medida do lado do quadrado PQRS é 3d e, portanto, sua área A é dada por:
Inscreva-se em nossa newsletter para receber atualizações sobre novas resoluções, dicas de estudo e informações que vão fazer a diferença na sua preparação!