Fique por dentro das novidades
Inscreva-se em nossa newsletter para receber atualizações sobre novas resoluções, dicas de estudo e informações que vão fazer a diferença na sua preparação!

A figura mostra o projeto de um portal construído de modo que um arco de parábola seja posicionado sobre uma estrutura retangular.
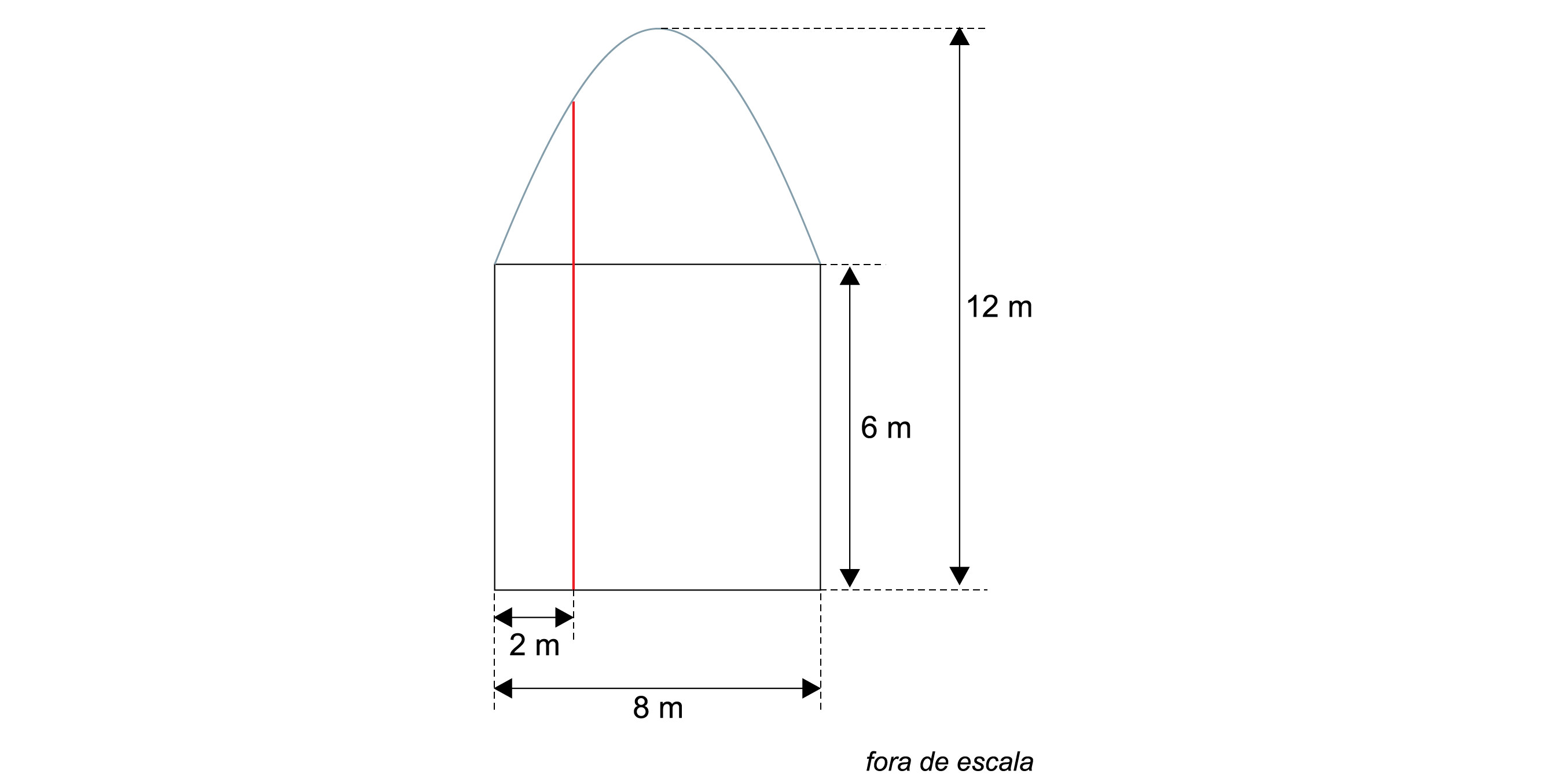
A estrutura retangular tem base medindo 8 m e altura de 6 m. O ponto mais alto do portal dista 12 m da base. Deseja-se adicionar uma coluna vertical, destacada em vermelho na figura, cuja base dista 2 m de uma das laterais da estrutura retangular. A altura da coluna será de
9,75 m.
7,50 m.
8,25 m.
10,50 m.
9,00 m.
Para descobrir a altura da coluna destacada em vermelho, é preciso encontrar uma lei de formação para o arco de parábola situada acima da estrutura retangular.
Para isso, fixa-se um sistema de coordenadas ortogonais, conforme a figura a seguir:
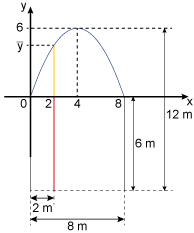
A lei de formação de uma função quadrática é da forma , em que e são as raízes da função, que, neste caso, são 0 e 8. Assim:
Para encontrar o coeficiente , basta substituir as coordenadas do ponto (4, 6) que pertence à parábola. Assim:
Portanto, .
Substituindo x = 2 na equação anterior, encontra-se:
.
Logo, a altura da coluna vertical destacada em vermelho tem comprimento de 6 + 4,50 =
Inscreva-se em nossa newsletter para receber atualizações sobre novas resoluções, dicas de estudo e informações que vão fazer a diferença na sua preparação!