Fique por dentro das novidades
Inscreva-se em nossa newsletter para receber atualizações sobre novas resoluções, dicas de estudo e informações que vão fazer a diferença na sua preparação!

No plano cartesiano, a reta r, de equação , intersecta a reta s, de equação y = x + 5, no ponto P. A reta r intersecta o eixo x no ponto R, e a reta s intersecta o eixo y no ponto S, como na figura.
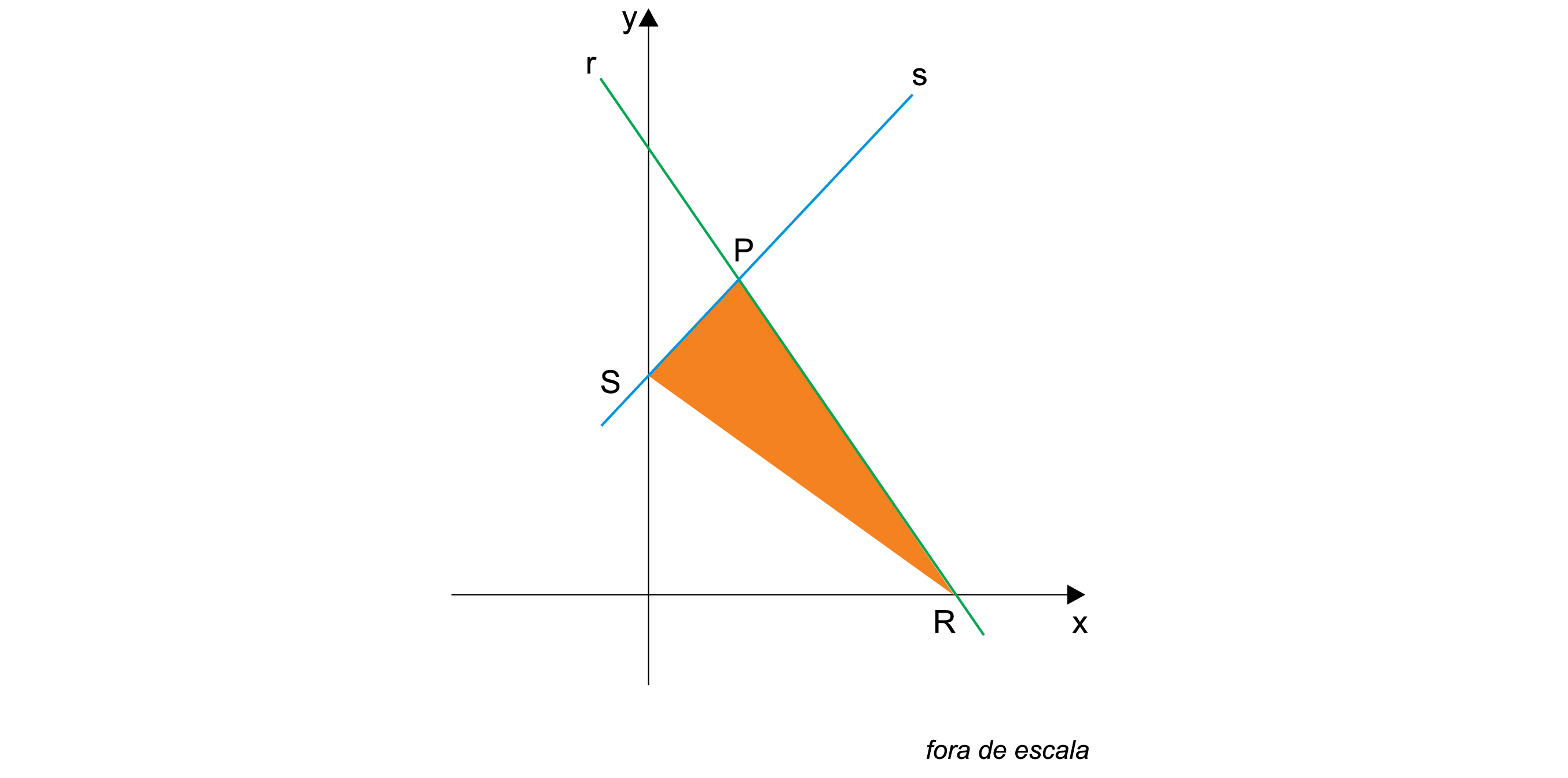
A área do triângulo de vértices PRS é
O ponto P é a interseção entre as retas r: e s: y = x + 5, assim
Substituindo x = 2 em qualquer uma destas equações, conclui-se que y = 0. Logo, P (2, 7).
O ponto R é a interseção da reta r com o eixo x, ou seja, fazendo y = 0 na equação da reta r: , conclui-se que . Logo, R = .
O ponto S é a interseção da reta s com o eixo y, ou seja, fazendo x = 0 na equação da reta s: y = x + 5, conclui-se que y = 5. Logo, S = (0, 5).
A área A do triângulo de vértices PRS é dada por , em que
.
Portanto,
Inscreva-se em nossa newsletter para receber atualizações sobre novas resoluções, dicas de estudo e informações que vão fazer a diferença na sua preparação!