Fique por dentro das novidades
Inscreva-se em nossa newsletter para receber atualizações sobre novas resoluções, dicas de estudo e informações que vão fazer a diferença na sua preparação!

Observe a figura abaixo.
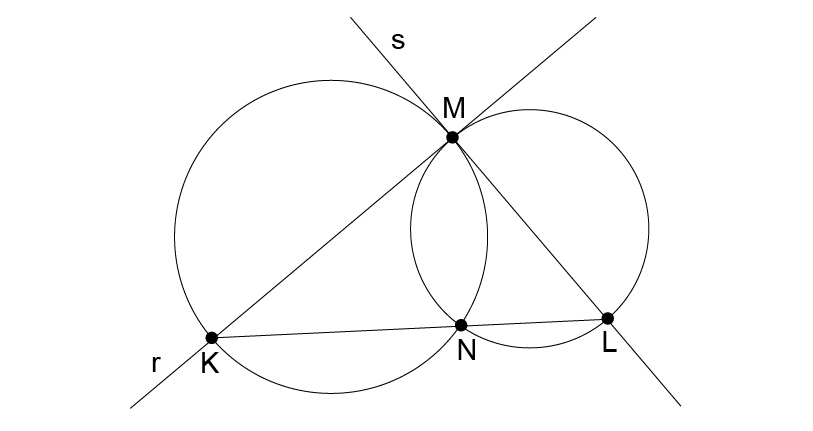
Na figura fora de escala tem-se duas circunferências secantes nos pontos M e N, as retas r e s tangentes às circunferências menor e maior, respectivamente, com e os pontos K, N e L alinhados.
Os segmentos , e medem, em cm, respectivamente, x + 5, x e 2x.
Analise as afirmativas a seguir, para as medidas dos segmentos em cm.
É correto afirmar que
nenhuma afirmativa é verdadeira.
apenas uma afirmativa é verdadeira.
apenas duas afirmativas são verdadeiras.
todas as afirmativas são verdadeiras.

Como os segmentos e são tangentes às circunferências no mesmo ponto M, eles são ortogonais entre si. Além disso, como o segmento KM faz 90° com a reta tangente, o segmento KM passa pelo centro da circunferência, sendo um diâmetro. A mesma justificativa é válida para o segmento LM. Como LM e KM são diâmetros, os ângulos MNL e MNK são de 90°.
Dessa forma, por Pitágoras, tem-se:
Das propriedades dos triângulos retângulos, tem-se:
Assim, , , e KM é obtido por Pitágoras:
Afirmativa I: correta. .
Afirmativa II: correta. .
Afirmativa III: correta. Pelas propriedades dos triângulos retângulos, infere-se que os triângulos são semelhantes.
Portanto, todas as afirmativas são verdadeiras.
Inscreva-se em nossa newsletter para receber atualizações sobre novas resoluções, dicas de estudo e informações que vão fazer a diferença na sua preparação!