Questão 28 - Prova Modelo A - AFA 2026

Primeiramente, analisam-se as condições de existência:

${\mathrm{x}}^2-3\mathrm{x} + 2 > 0 \Rightarrow \left(\mathrm{x}-1\right)\left(\mathrm{x}-2\right) > 0 \Rightarrow \mathrm{x} < 1 \mathrm{ou} \mathrm{x} > 2$

$-{\mathrm{x}}^2+ 2\mathrm{x} > 0 \Rightarrow 0 < \mathrm{x} < 2$

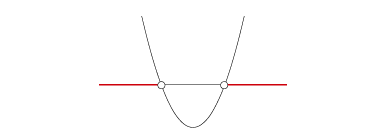
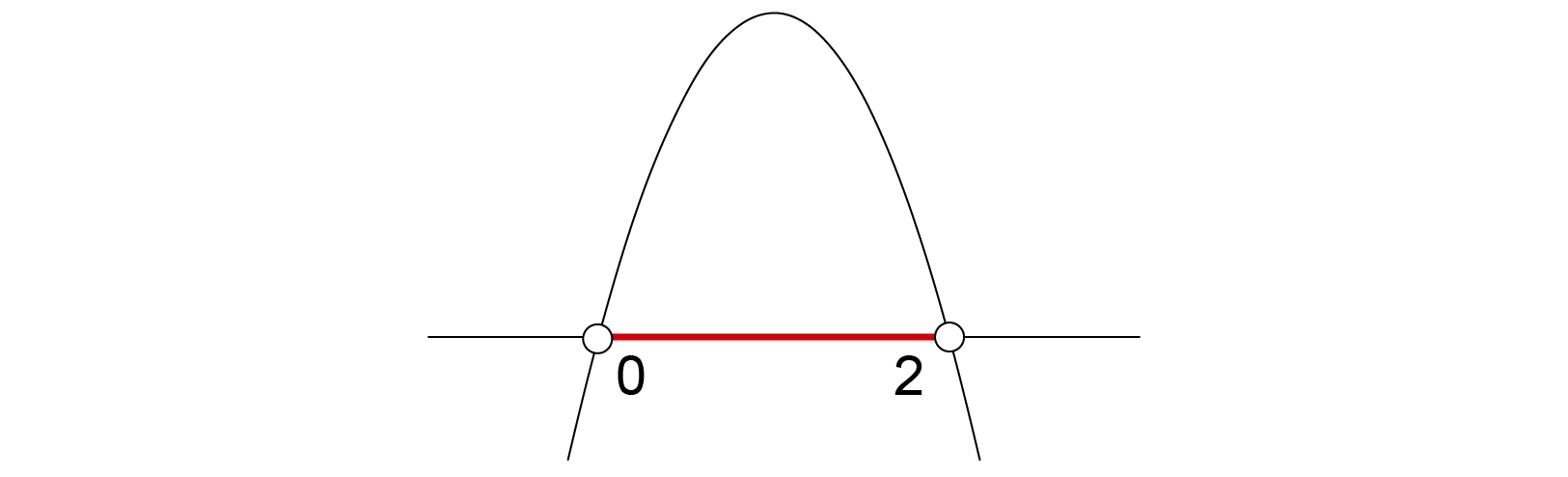
Feitas as condições de existência, conclui-se a análise. Se $\frac{1}{3}$ é solução da equação, tem-se:

$$\begin{gathered} {\log }_{\mathrm{b}}\left({\left(\frac{1}{3}\right)}^2-3·\frac{1}{3}+2\right) < {\log }_{\mathrm{b}}\left(-{\left(\frac{1}{3}\right)}^2+2·\frac{1}{3}\right) \\ {\log }_{\mathrm{b}}\frac{10}{9} < {\log }_{\mathrm{b}}\frac{5}{9} \\ 0 < \mathrm{b} < 1 \end{gathered}$$

Assim, a solução da equação será:

$$\begin{gathered} {\mathrm{x}}^2-3\mathrm{x} + 2 >-{\mathrm{x}}^2+ 2\mathrm{x} \\ 2{\mathrm{x}}^2- 5\mathrm{x} + 2 > 0 \\ 2 · \left(\mathrm{x} - 2\right)\left(\mathrm{x} - \frac{1}{2}\right) > 0 \end{gathered}$$

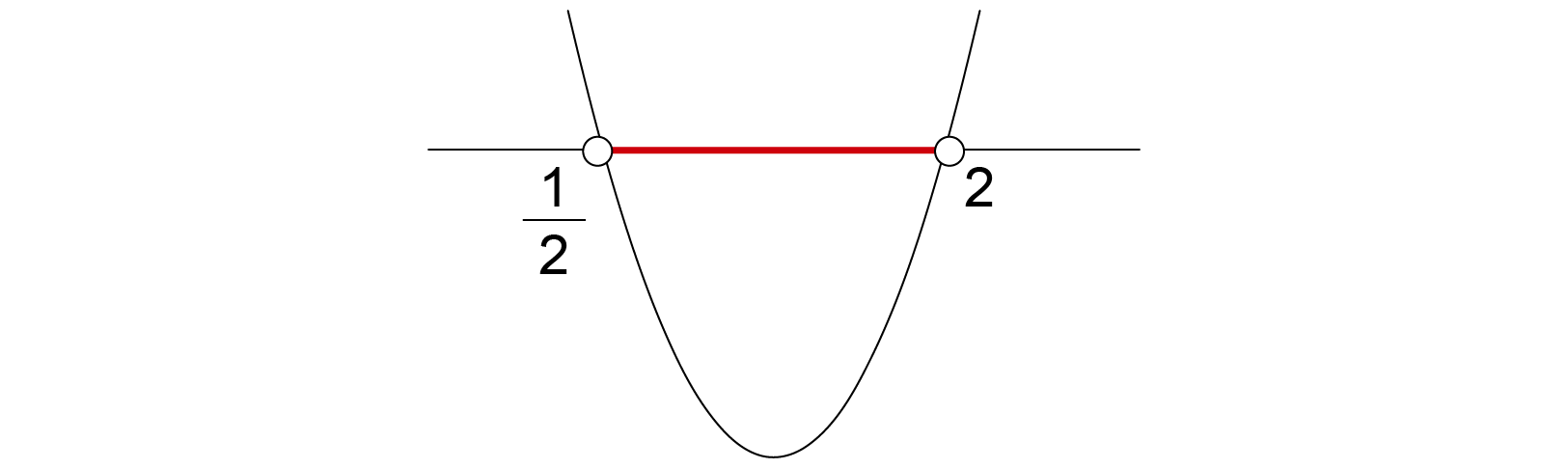
Fazendo a interseção de todas as condições, tem-se:

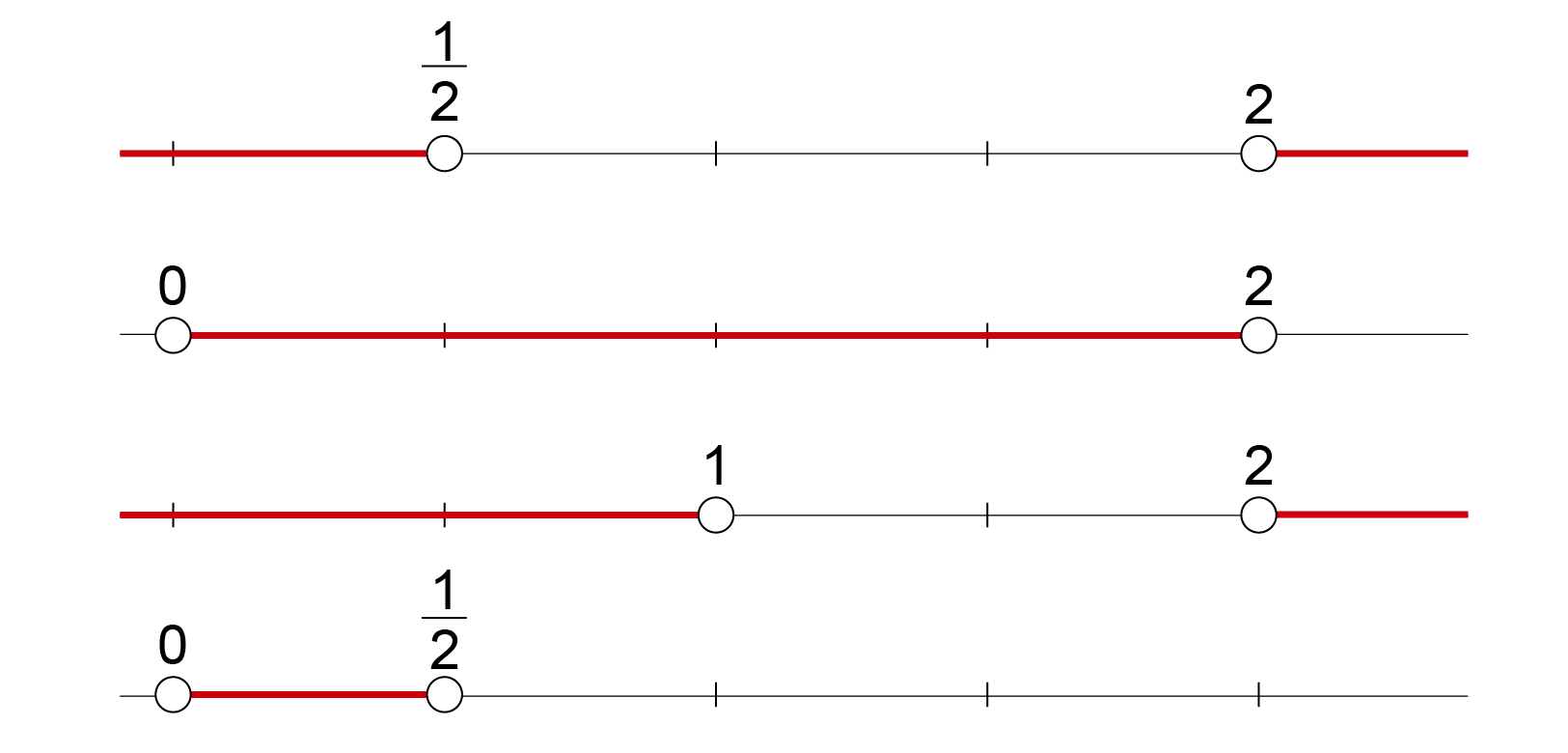
Assim, o conjunto solução é: 

$\boxed{0 < \mathrm{x} < \frac{1}{2}}$