Questão 17 - Prova Modelo A - AFA 2026

Selecione uma prova

Gabarito

Geral
1. 1C
2. 2C
3. 3A
4. 4D
5. 5C
6. 6B
7. 7A
8. 8D
9. 9C
10. 10B
11. 11C
12. 12D
13. 13D
14. 14B
15. 15D
16. 16C
17. 17D
18. 18D
19. 19A
20. 20C
21. 21A
22. 22C
23. 23B
24. 24B
25. 25B
26. 26A
27. 27B
28. 33B
29. 34C
30. 35B
31. 36C
32. 37D
33. 38D
34. 39D
35. 40C
36. 41A
37. 42A
38. 43C
39. 44D
40. 45C
41. 46A
42. 47D
43. 48B

Questão ativa
Já visualizadas
Não visualizadas
Resolução pendente
ANL
Questão anulada
S/A
Sem alternativas

Questão 17

Objetiva

Observe a figura abaixo na qual está representada uma esfera com uma parte inserida em um recipiente em formato de tronco de cone.

A esfera está tangente à base menor desse tronco e também à borda superior do recipiente.

Se os raios maior, menor e a altura do recipiente são, respectivamente, 2x cm, (x + 2) cm e x cm, e se o volume do que sobra do recipiente, ao ser inserida a esfera, é igual a 420 cm³, considerando $π = 3$ , então, é correto afirmar que a área da esfera, em cm², é igual a

Alternativas

A
432
B
972
C
1728
D
2700

Gabarito:
D

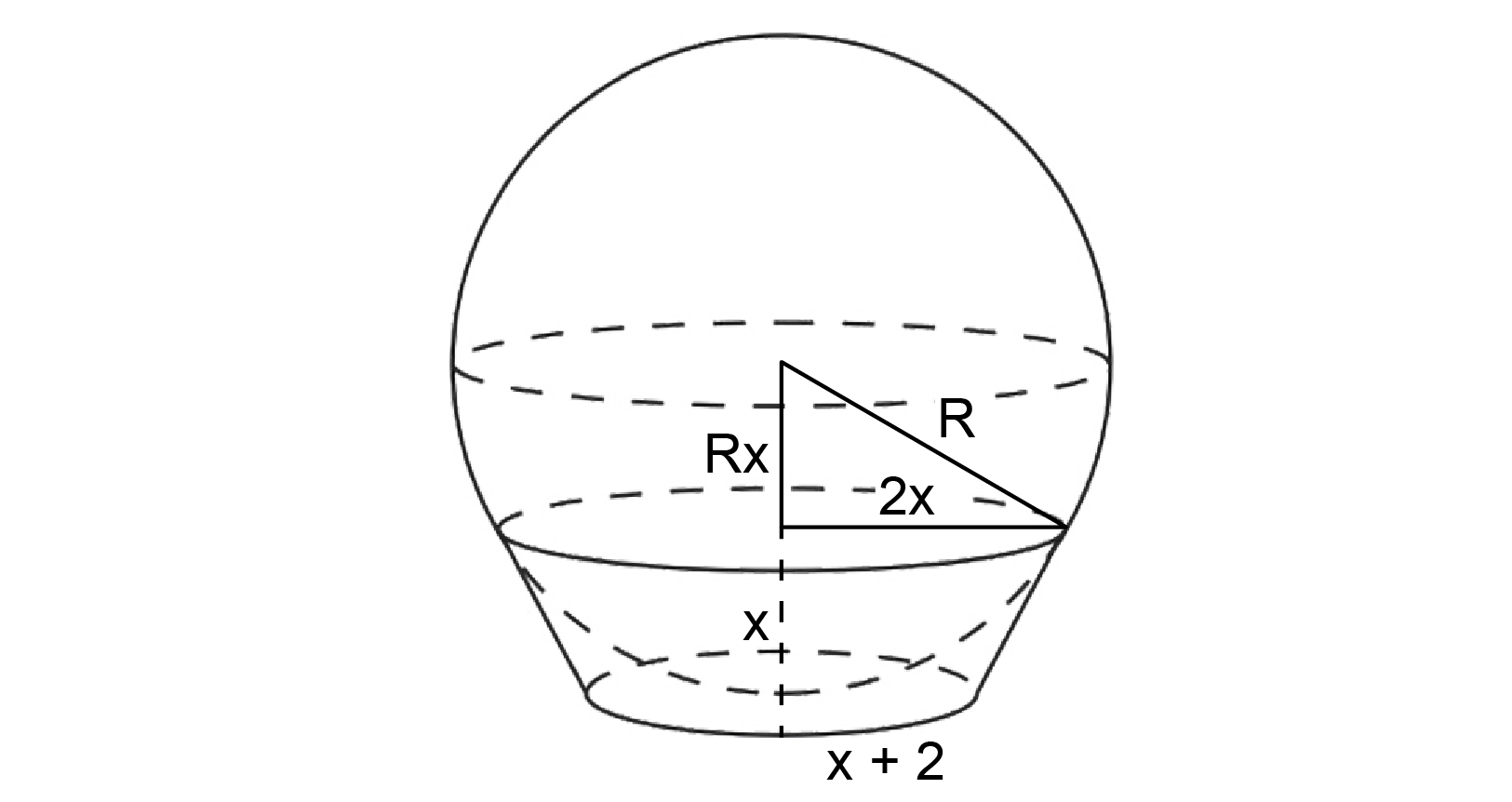
Da imagem, é possível montar o seguinte teorema de Pitágoras:

$R^{2} = {(R - x)}^{2} + {(2 x)}^{2} R^{2} = R^{2} - 2 Rx + x^{2} + 4 x^{2} x = \frac{2 R}{5} V_{calota esférica} = \frac{π}{3} \cdot h^{2} \cdot (3 R - h), em que h é a altura da calota . V_{calota esférica} = \frac{π}{3} \cdot \frac{2 R^{2}}{5} \cdot (3 R - \frac{2 R}{5}) = \frac{52 R^{3}}{125} V_{Tronco de cone} = \frac{πh}{3} \cdot (R_{maior}^{2} + R_{maior} r_{menor} + r_{menor}^{2}) = = \frac{πh}{3} \cdot ({(\frac{2 \cdot 2 R}{5})}^{2} + (\frac{2 \cdot 2 R}{5}) (\frac{2 R}{5} + 2) + {(\frac{2 R}{5} + 2)}^{2}) = = \frac{\frac{π}{3} (56 R^{3} + 160 R^{2} + 200 R)}{125}$

Como $V_{vazio} = V_{tronco de cone} - V_{Calota esférica} e π = 3$ , tem-se:

$V_{vazio} = 420 = \frac{56 R^{3} + 160 R^{2} + 200 R - 52 R^{3}}{125} = \frac{4 R^{3} + 160 R^{2} + 200 R}{125} \frac{4 R^{3} + 160 R^{2} + 200 R}{125} = 420 \Rightarrow R^{3} + 40 R^{2} + 50 R = 105 \cdot 125 R^{3} + 40 R^{2} + 50 R - 105 \cdot 125 = 0 \Rightarrow (R - 15) \cdot (R^{2} + 55 R + 875) = 0 \Rightarrow R = 15 Área da esfera = 4 {πR}^{2} = 4 \cdot 3 \cdot {(15)}^{2} = 2700$

Fique por dentro das novidades

Inscreva-se em nossa newsletter para receber atualizações sobre novas resoluções, dicas de estudo e informações que vão fazer a diferença na sua preparação!