Fique por dentro das novidades
Inscreva-se em nossa newsletter para receber atualizações sobre novas resoluções, dicas de estudo e informações que vão fazer a diferença na sua preparação!

Sejam as raízes do polinômio com
Considere, no ciclo trigonométrico, os arcos dados por e
Considere, também, A, B, C e D os pontos de extremidades dos arcos , respectivamente, no sentido anti-horário, com origem no ponto de coordenadas
Analise as afirmações a seguir.
(I) A sequência é uma progressão geométrica.
(II) A sequência é uma progressão aritmética.
(III) A área do polígono ABCD é igual a unidades de área.
É correto afirmar que
nenhuma afirmativa é verdadeira.
apenas uma afirmativa é verdadeira.
apenas duas afirmativas são verdadeiras.
todas as afirmativas são verdadeiras.
Dado o polinômio , tem-se as seguintes raízes:
Analisando as afirmativas:
Afirmativa I: incorreta.
Afirmativa II: incorreta.
Afirmativa III: correta. No ciclo trigonométrico, tem-se:
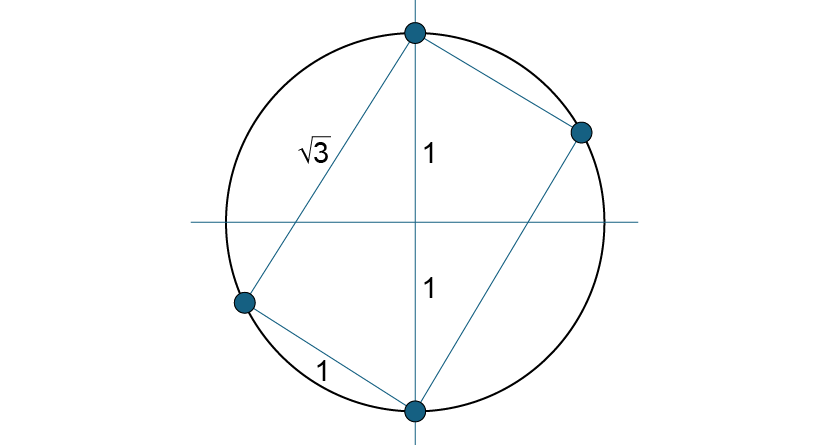
O qual é um quadrado cuja área é unidades de área.
Portanto, apenas uma afirmativa é verdadeira.
Inscreva-se em nossa newsletter para receber atualizações sobre novas resoluções, dicas de estudo e informações que vão fazer a diferença na sua preparação!