Fique por dentro das novidades
Inscreva-se em nossa newsletter para receber atualizações sobre novas resoluções, dicas de estudo e informações que vão fazer a diferença na sua preparação!
Questão ativa
Já visualizadas
Não visualizadas
Resolução pendente
Questão anulada
Sem alternativas

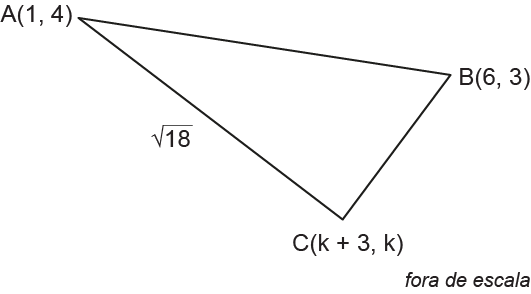
Considere, em um plano cartesiano, o triângulo ABC, com A(1, 4), B(6, 3) e C(k + 3, k), em que k é um número real, de modo que a distância entre os vértices A e C seja .
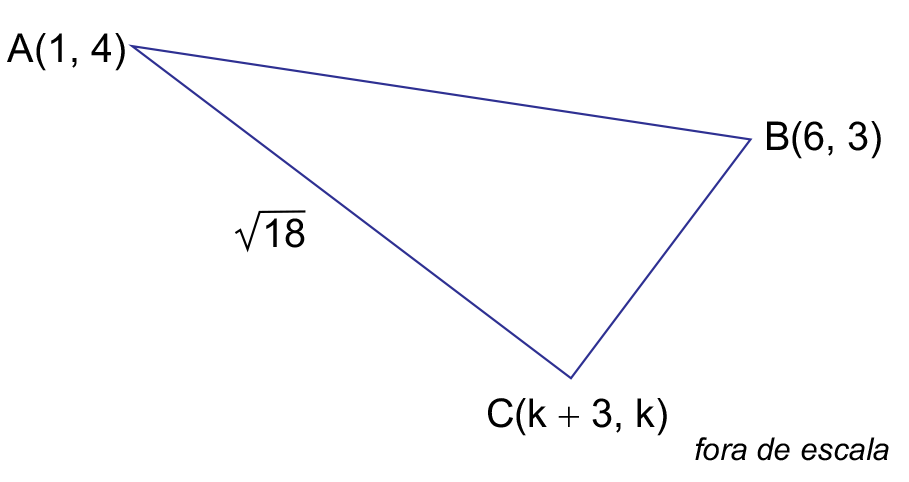
A equação da reta que passa pelos pontos B e C é:
Elevando os dois lados da equação ao quadrado, tem-se: e desenvolvendo os trinômios: ; resolvendo a equação do segundo grau na variável k, obtém-se k = 1, ou seja, C (4, 1).
Cálculo da equação da reta que passa pelos pontos B e C:
Inscreva-se em nossa newsletter para receber atualizações sobre novas resoluções, dicas de estudo e informações que vão fazer a diferença na sua preparação!