Fique por dentro das novidades
Inscreva-se em nossa newsletter para receber atualizações sobre novas resoluções, dicas de estudo e informações que vão fazer a diferença na sua preparação!

O “efeito estilingue” é o nome que se dá à modificação do módulo e da direção da velocidade de uma espaçonave quando ela passa nas imediações de um planeta. Ele foi utilizado, por exemplo, para encurtar em mais de 5 anos a duração da viagem da sonda New Horizons até Plutão, passando por Júpiter. A figura ao lado ilustra o efeito em uma situação na qual uma sonda de massa 500 kg, viajando inicialmente para a direita, move-se em direção a um planeta de massa kg que viaja para a esquerda. Como a massa da sonda é desprezível frente à do planeta, a trajetória deste último praticamente não se altera, embora parte de sua energia cinética seja transferida para a sonda. Nos pontos 𝐴 e 𝐵 indicados na figura, as distâncias entre a sonda e o planeta são tais que a energia potencial gravitacional associada à interação entre eles pode ser desprezada.
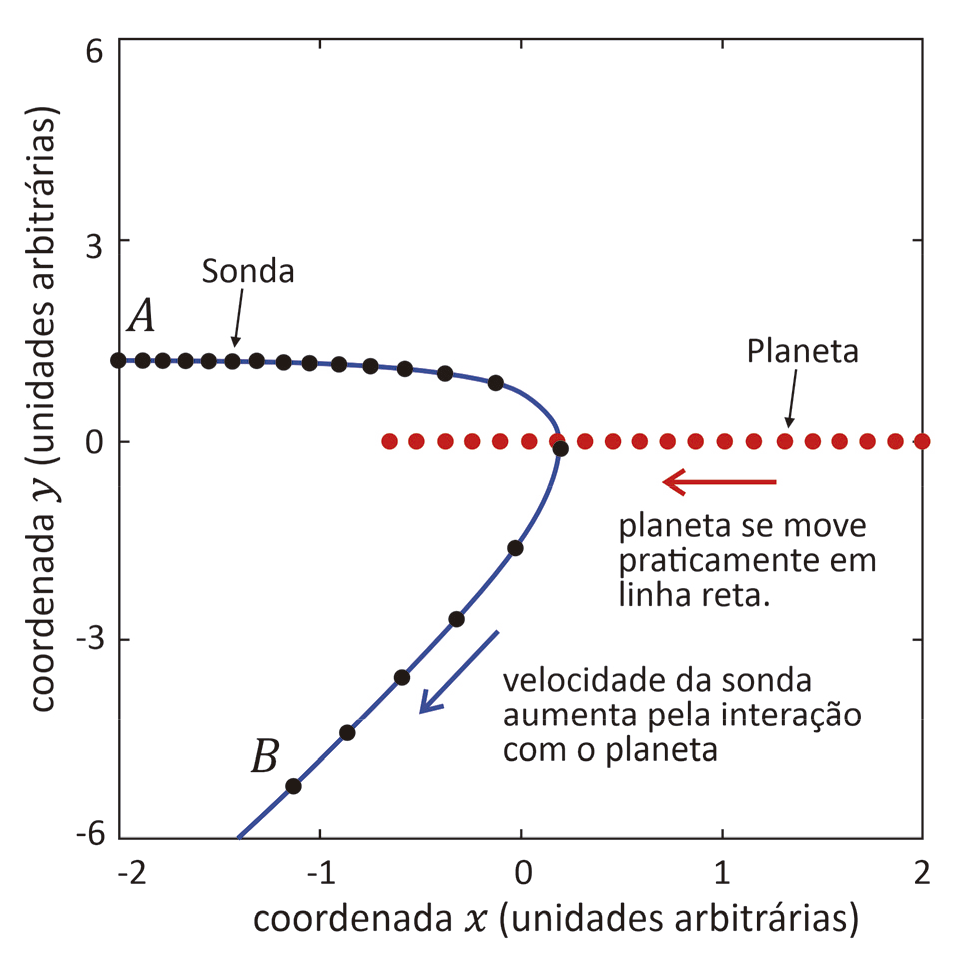
a) No ponto 𝐴, a velocidade da sonda em relação ao Sol tem apenas componente 𝑥, dada por 20 km/s, enquanto essa velocidade no ponto 𝐵 é , com componente 𝑥 igual a –7 km/s e componente 𝑦 igual a –24 km/s. De quanto foi o aumento no módulo da velocidade da sonda entre esses dois pontos?
b) Nas mesmas condições do item anterior, determine as componentes 𝑥 e 𝑦 do vetor variação da quantidade de movimento da sonda entre os pontos 𝐴 e 𝐵, bem como a tangente do ângulo entre esse vetor e o eixo 𝑥.
c) Nas mesmas condições dos itens anteriores, qual é a razão entre a variação da energia cinética do planeta e sua energia cinética inicial? Suponha que o módulo da velocidade inicial do planeta, em relação ao Sol, fosse de 5 km/s. Despreze a variação da energia potencial gravitacional associada à interação da sonda e do planeta com o Sol durante o processo.
a.
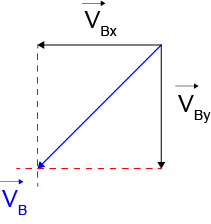
b.
I. Determinar o
– 7 km/s (vetor com sentido para a esquerda)
20 km/s (vetor com sentido para a direita)
II. Determinar o
III. Determinar a tangente do ângulo:
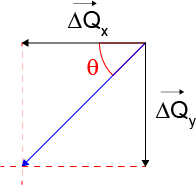
c.
I. Determinar a variação de energia cinética do planeta, convertendo as grandezas para o sistema internacional de unidades:
II. Determinar a energia cinética inicial do planeta:
III. Determinar a razão solicitada:
Inscreva-se em nossa newsletter para receber atualizações sobre novas resoluções, dicas de estudo e informações que vão fazer a diferença na sua preparação!