Dissertativas 4 - Dia 2 - Fuvest 2025

Poliedro Resolve - Resoluções - Fuvest 1ª Fase - 2025

Selecione uma prova

Gabarito

Biologia
1. 3DIS
2. 4DIS
3. 5DIS
4. 6DIS
Física
1. 1DIS
2. 2DIS
3. 3DIS
4. 4DIS
5. 5DIS
6. 6DIS
Geografia
1. 1DIS
2. 2DIS
3. 3DIS
4. 4DIS
5. 5DIS
História
1. 1DIS
2. 2DIS
3. 3DIS
4. 4DIS
5. 5DIS
6. 6DIS
Matemática
1. 1DIS
2. 2DIS
3. 3DIS
4. 4DIS
Química
1. 1DIS
2. 2DIS
3. 3DIS
4. 4DIS
5. 5DIS
6. 6DIS

Questão ativa
Já visualizadas
Não visualizadas
Resolução pendente
ANL
Questão anulada
S/A
Sem alternativas

Questão 4

Dissertativa

Ondas sísmicas são ondas que se propagam em camadas de rochas no interior do manto da Terra. Essas ondas podem ser longitudinais (como o som, por exemplo) ou transversais (como as ondas que se propagam em uma corda). Um tipo de onda sísmica transversal é a chamada onda secundária (ou “onda S” ou “onda de cisalhamento”) e sua velocidade é dada por

$v_{s} = \sqrt{\frac{μ}{ρ}},$

em que $μ$ é o módulo de cisalhamento e $ρ$ é a densidade (ou massa específica), parâmetros da rocha em que a onda se propaga.

a) Através de uma análise dimensional, determine a unidade do módulo de cisalhamento $μ$ no Sistema Internacional de Unidades (SI).

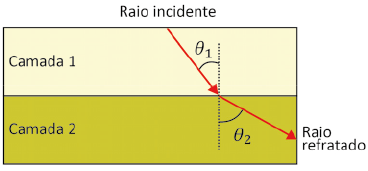
Na interface entre dois tipos de rocha, pode haver refração das ondas sísmicas, e a mudança de direção é dada pela Lei de Snell, conforme mostra o exemplo da figura a seguir.

$\frac{sen θ_{1}}{v_{s_{1}}} = \frac{sen θ_{2}}{v_{s_{2}}}$

Velocidades de ondas S típicas de alguns materiais comuns no manto terrestre são dadas na tabela a seguir.

Material	Granito	Basalto	Arenito	Calcário	Argila
Velocidade da onda S (m/s)	2900	2600	1400	2700	700

Fontes: https://gpg.geosci.xyz/content/physical_properties/seismic_velocity_duplicate.html
https://pburnley.faculty.unlv.edu/GEOL452_652/seismology/notes/SeismicNotes10RVel.html

Considere uma onda S harmônica de frequência 0,3 Hz propagando-se através de uma interface entre duas camadas com composições diferentes.

b) Se a camada 1 for predominantemente composta por basalto e a camada 2 por granito, qual será a variação no comprimento de onda, $λ_{2} - λ_{1} ?$
c) Em outra interface, são medidos $sen θ_{1} = 0, 26 e sen θ_{2} = 0, 52 .$ Se a camada 1 for composta predominantemente de argila, qual será, dentre os materiais apresentados na tabela, aquele que melhor corresponderá à composição da camada 2? Justifique a sua resposta.

Note e adote:

Unidade de densidade (massa específica) no SI: $kg / m^{3}$ .

Resolução:

a. A partir da expressão da velocidade apresentada, pode-se obter o valor do módulo de cisalhamento $(μ)$ em função da velocidade $(ν)$ e da densidade $(ρ)$ :

$v = \sqrt{\frac{μ}{ρ}} \Leftrightarrow v^{2} = \frac{μ}{ρ} \Leftrightarrow μ = ρ \cdot v^{2}$

Assim, fazendo a análise dimensional de cada grandeza, tem-se:

$[ρ] = M \cdot L^{- 3} [v] = L \cdot T^{- 1}$

$[μ] = M \cdot L^{- 3} \cdot {(L \cdot T^{- 1})}^{2} \Rightarrow [μ] = M \cdot L^{- 3} \cdot L^{2} \cdot T^{- 2} \Rightarrow [μ] = M \cdot L^{- 1} \cdot T^{- 2} (equação dimensional do módulo de cisalhamento)$

É importante ressaltar que, nas equações dimensionais, M, L e T representam massa, comprimento e tempo, respectivamente. A partir dessas grandezas fundamentais da mecânica, pode-se escrever qualquer outra grandeza. Assim, utiliza-se essa notação para realizar a análise de unidades.

A partir da equação dimensional do cisalhamento, sua unidade é dada por:

$[μ] = M \cdot L^{- 1} \cdot T^{- 2} \Rightarrow [μ] = kg \cdot m^{- 1} \cdot s^{- 2} = \frac{kg}{m \cdot s^{2}}$

b. Pela equação fundamental da ondulatória, pode-se determinar o comprimento de onda nas camadas 1 e 2:

$λ_{1} = \frac{v_{1}}{f_{1}} = \frac{2 600}{0, 3} λ_{2} = \frac{v_{2}}{f_{2}} = \frac{2 900}{0, 3}$

Denota-se $f_{1} = f_{2}$ , pois, na refração, a frequência não se altera (pois depende apenas da fonte).

Assim, a diferença $λ_{2} - λ_{1}$ é dada por:

$λ_{2} - λ_{1} = \frac{2 900}{0, 3} - \frac{2 600}{0, 3} = \frac{300}{0, 3} \Rightarrow λ_{2} - λ_{1} = 1 000 m$

c. A partir da lei de Snell, pode-se determinar a velocidade na camada 2 ( $v_{2}$ ):

$\frac{sen (θ_{1})}{ν_{1}} = \frac{sen (θ_{2})}{ν_{2}} \Rightarrow \frac{0, 26}{700} = \frac{0, 52}{ν_{2}} \Rightarrow ν_{2} = \frac{0, 52 \cdot 700}{0, 26} \Rightarrow ν_{2} = 1 400 m / s$

Portanto, com base nos dados da tabela, conclui-se que o material da camada 2 é o arenito.

Downloads

Provas

Fique por dentro das novidades

Inscreva-se em nossa newsletter para receber atualizações sobre novas resoluções, dicas de estudo e informações que vão fazer a diferença na sua preparação!

Dissertativas 4 - Dia 2 - Fuvest 2025

Gabarito

Biologia

Física

Geografia

História

Matemática

Química

Questão 4

Resolução:

Downloads

Provas

Fique por dentro das novidades