Fique por dentro das novidades
Inscreva-se em nossa newsletter para receber atualizações sobre novas resoluções, dicas de estudo e informações que vão fazer a diferença na sua preparação!

No plano, o segmento PS intersecta os lados do quadrado ABCD nos pontos Q e R, conforme a figura.
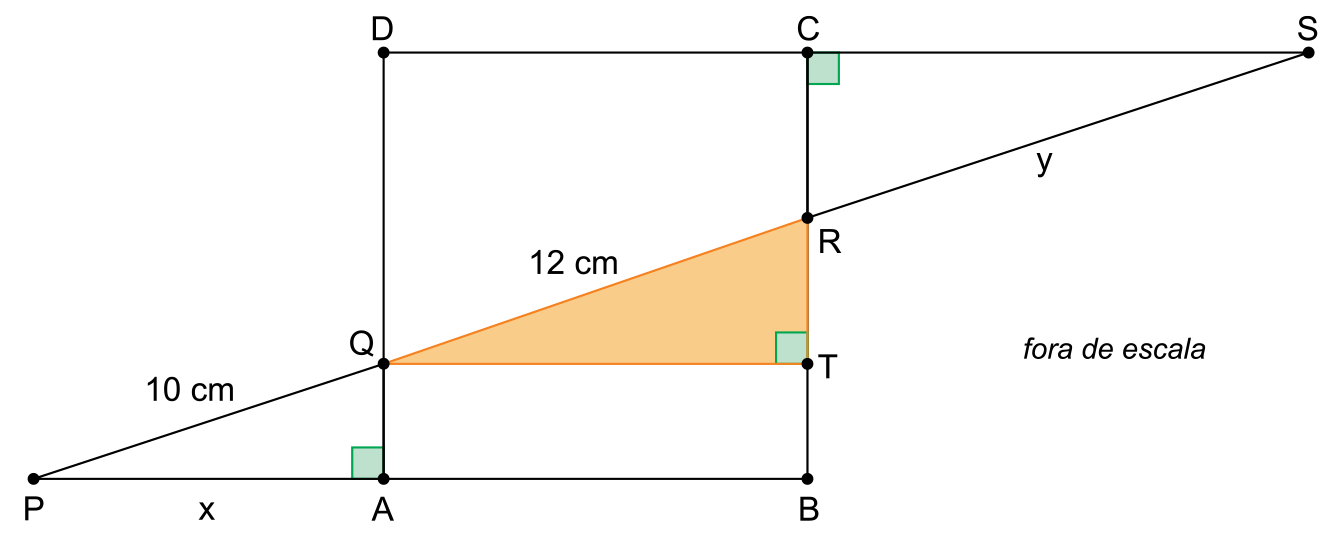
a) Se a medida x do segmento PA for igual a 9 cm, qual será a área do quadrado ABCD?
b) Se a medida e o segmento RS for igual a 14 cm, qual será a área do triângulo QRT?
a) Sendo x = 9 cm, por semelhança de triângulos entre APQ e TQR, tem-se:
Portanto, como QT = AB, conclui-se que, nessa situação, a área do quadrado ABCD é igual a (10,8)² = .
b) Como os segmentos , e são paralelos entre si e são interceptados pelo segmento transversal , infere-se que med( ) = med() = med() = θ.
Assim, sendo L a medida do lado do quadrado ABCD, como QT = AB = L, tem-se:
L = 12 · cos(θ)
Como os segmentos e são paralelos, AQ = BT. Assim, sendo RS = y = 14 cm, a medida do lado do quadrado ABCD pode ser expressa por:
BC = L = BT + TR + RC ⇒ L = 10 · sen(θ) + 12 · sen(θ) + 14 · sen(θ) ⇒ L = 36 · sen(θ)
Ao igualar as duas equações obtidas para o valor de L, tem-se:
12 · cos(θ) = 36 · sen(θ) ⇒ ⇒ tg(θ) =
Como a tangente de um ângulo interno em um triângulo retângulo corresponde à razão entre as medidas de seus catetos, pode-se considerar θ um ângulo interno do triângulo retângulo mostrado a seguir.
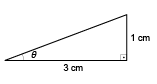
Nesse triângulo, a medida x da hipotenusa é dada, em centímetro, por:
x² = 1² + 3² ⇒ x = cm
Logo, o seno e o cosseno de θ são dados por:
sen(θ) =
cos(θ) =
A área do triângulo QRT é expressa por:
Desse modo, como QT = 12 · cos(θ) e RT = 12 · sen(θ), tem-se:
Inscreva-se em nossa newsletter para receber atualizações sobre novas resoluções, dicas de estudo e informações que vão fazer a diferença na sua preparação!