Fique por dentro das novidades
Inscreva-se em nossa newsletter para receber atualizações sobre novas resoluções, dicas de estudo e informações que vão fazer a diferença na sua preparação!

Um lago artificial tem a forma de prisma reto, cuja base é o polígono UNIFESP, com UN = UP = 6 m, NI = PS = 2 m, IF = 1m, e ângulos indicados na figura.
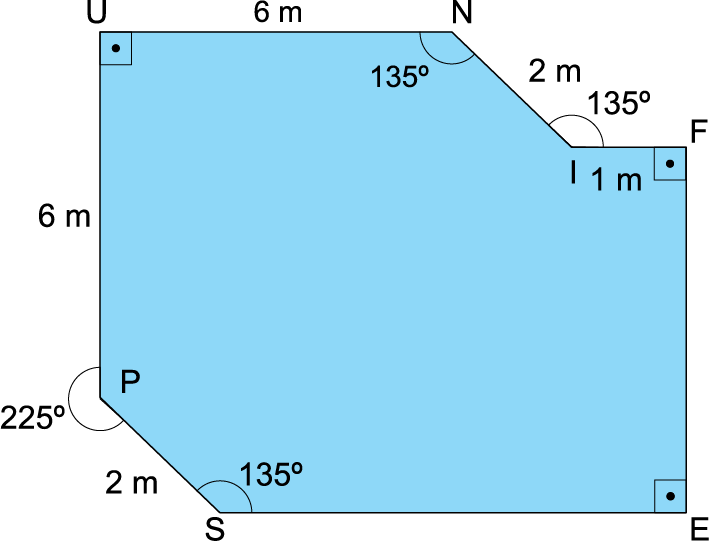
a) Calcule as medidas de e , ambas em metros.
b) Calcule a altura aproximada do lago, em centímetros e com uma casa decimal depois da vírgula, sabendo que o volume do lago é igual a .
a) Observe a figura a seguir, em que A e B são vértices de um retângulo de diagonal SP = 2 m e C e D são vértices de um retângulo de diagonal NI = 2 m:
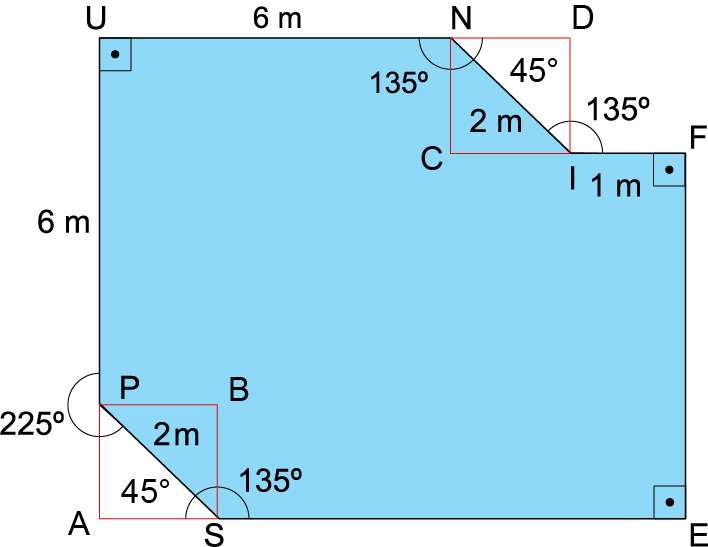
Como e , infere-se que os quadriláteros APBS e CNDI são quadrados. Dado que a diagonal de um quadrado de lado x mede , infere-se que ambos os quadrados indicados têm lados cuja medida é dada por:
Pela imagem, UN + CI + IF = AS + SE. Logo:
6 + + 1 = + SE
Pela imagem, DI + FE = UP + PA. Logo:
+ FE = 6 +
b) Na figura a seguir, a área da base do lago corresponde à área do retângulo AUGE subtraída das áreas do triângulo ASP e do trapézio FING.
__5f0f0bdb-e575-4c8c-972b-0dcfa43c8661.png)
Logo:
Como o volume do prisma é dado pelo produto entre a área da base do lago e a altura do mesmo, tem-se:
Portanto, a altura do lago vale, aproximadamente, .
Inscreva-se em nossa newsletter para receber atualizações sobre novas resoluções, dicas de estudo e informações que vão fazer a diferença na sua preparação!