Fique por dentro das novidades
Inscreva-se em nossa newsletter para receber atualizações sobre novas resoluções, dicas de estudo e informações que vão fazer a diferença na sua preparação!

Em uma partida de sinuca, a bola branca (B) é lançada com velocidade contra a bola azul (A), inicialmente em repouso (), no centro da mesa, conforme a figura 1. Após a colisão, as bolas movem-se perpendicularmente uma a outra, com velocidades constantes e , conforme a figura 2, e a bola azul cai na caçapa C.
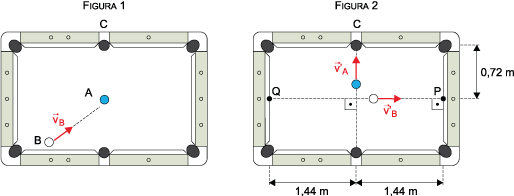
Admita que as massas das bolas são iguais, que nessa jogada o atrito é desprezível e que todas as colisões são perfeitamente elásticas. Calcule, em segundos, o tempo para que:
a) a bola branca atinja o ponto P, indicado na figura 2, após sua colisão com a bola azul. Em seguida, calcule o tempo para que a bola branca percorra a distância PQ, indicada na figura 2, após sua reflexão no ponto P.
b) a bola azul caia na caçapa C, após ser atingida pela bola branca.
a) Calculando-se, primeiramente, o tempo para que a bola branca atinja o ponto P após sua colisão com a bola azul, tem-se:
Note que o tempo necessário para que a bola branca percorra a distância PQ é exatamente o dobro do tempo , pois, após a reflexão no ponto P, a bola retornará ao ponto central da mesa (região que ocorreu a colisão com a bola A) e depois percorrerá a mesma distância que percorreu do centro da mesa até o ponto P. Logo, tem-se que:
b) Como a colisão é perfeitamente elástica, de acordo com o enunciado, pode-se usar a conservação do momento linear do sistema para o cálculo de , da seguinte maneira:
Como as massas são iguais para as duas bolas (branca e azul), pode-se simplificá-las na expressão acima. Além disso, a bola A se encontra inicialmente em repouso , logo, tem-se:
Como são vetores perpendiculares, temos:
Portanto, calculando-se o tempo para que a bola azul caia na caçapa C, após ser atingida pela bola branca, tem-se:
Inscreva-se em nossa newsletter para receber atualizações sobre novas resoluções, dicas de estudo e informações que vão fazer a diferença na sua preparação!