Dissertativas 13 - Dia 2 - Unifesp 2025

Poliedro Resolve Resolução - Unifesp Dia 1 - 2025

Poliedro Resolve Resolução - Unifesp Dia 2 - 2025

Selecione uma prova

Gabarito

Geral
1. 1DIS
2. 2DIS
3. 3DIS
4. 4DIS
5. 5DIS
6. 6DIS
7. 7DIS
8. 8DIS
9. 9DIS
10. 10DIS
11. 11DIS
12. 12DIS
13. 13DIS
14. 14DIS
15. 15DIS
16. 16DIS
17. 17DIS
18. 18DIS
19. 19DIS
20. 20DIS

Questão ativa
Já visualizadas
Não visualizadas
Resolução pendente
ANL
Questão anulada
S/A
Sem alternativas

Questão 13

Dissertativa

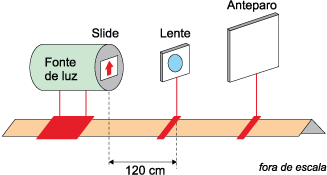
A figura mostra o esquema de um equipamento que permite o estudo de instrumentos e de fenômenos ópticos. Nessa figura, estão representados uma fonte de luz, uma lente convergente delgada e um anteparo. Movendo-se os suportes desses elementos, pode-se projetar uma imagem nítida de um slide na superfície do anteparo. Sabe-se que o eixo de simetria da fonte de luz coincide com o eixo principal da lente, que esse eixo é perpendicular ao plano que contém o anteparo, que a distância focal dessa lente é 40 cm e que ela obedece às condições de nitidez de Gauss.

Considere que o slide tenha 5 cm de altura e que inicialmente ele esteja fixo a 120 cm de distância do centro óptico da lente, também fixa.

a) Calcule a que distância da lente, em cm, deve ser colocado o anteparo, para que uma imagem nítida do slide seja projetada sobre ele. Em seguida, calcule a altura dessa imagem, em cm.

b) Mantendo a lente fixa, calcule qual deve ser a distância entre o slide e o anteparo, em cm, para que uma imagem nítida e duas vezes maior do que o slide seja projetada sobre o anteparo.

Resolução:

a) Sendo a lente convergente, ou seja, com distância focal positiva, tem-se pela relação de Gauss que:

$\frac{1}{f} = \frac{1}{p} + \frac{1}{p'}$

em que f é a distância focal, p a distância do objeto e p' a distância da imagem. Segundo o texto, f = 40 cm e p = 120 cm. Logo:

$\frac{1}{p'} = \frac{1}{f} - \frac{1}{p} = \frac{p - f}{fp} p' = \frac{fp}{p - f} p' = \frac{40 \cdot 120}{120 - 40} = \frac{40 \cdot 120}{80} p' = 60 cm$

Ainda de acordo com o texto, a altura do objeto (slide) é de 5 cm. Assim, pelo aumento linear:

$\frac{i}{o} = \frac{p'}{p} i = \frac{p'}{p} \cdot o = \frac{60}{120} \cdot 5 i = 2, 5 cm$

b) Para que o tamanho da imagem seja duas vezes maior do que o objeto, ele deve ser colocado entre o ponto antiprincipal e o foco da lente. Assim:

$\frac{i}{o} = 2 = \frac{p'}{p} p' = 2 p (I)$

Usando esse resultado na relação de Gauss:

$\frac{1}{f} = \frac{1}{p} + \frac{1}{p'} \frac{1}{f} = \frac{1}{p} + \frac{1}{2 p} = \frac{2}{2 p} + \frac{1}{2 p} = \frac{3}{2 p} p = \frac{3 f}{2} p = \frac{3 \cdot 40}{2} = 60 cm$

Usando esse resultado em I:

$p' = 2 \cdot 60 = 120 cm$

Logo, a distância entre o slide e o anteparo será:

$d = p + p' = 60 + 120 d = 180 cm$

Downloads

Provas

Fique por dentro das novidades

Inscreva-se em nossa newsletter para receber atualizações sobre novas resoluções, dicas de estudo e informações que vão fazer a diferença na sua preparação!