Dissertativa 6 - 2ª Fase - Dia 3 - ITA 2026

A figura a seguir ilustra o esquema de uma luneta astronômica:

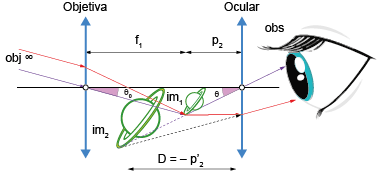
Aumento visual ou angular (em módulo):

$\mathrm{G}=\frac{\mathrm{\theta }}{{\mathrm{\theta }}_0}\cong \frac{\mathrm{tg\theta }}{{\mathrm{tg\theta }}_0}=\frac{{\displaystyle \raisebox{1ex}{${\mathrm{h}}_2$}\!\left/ \!\raisebox{-1ex}{$\mathrm{D}$}\right.}}{{\displaystyle \raisebox{1ex}{${\mathrm{h}}_1$}\!\left/ \!\raisebox{-1ex}{${\mathrm{f}}_1$}\right.}}=\frac{{\mathrm{f}}_1}{\mathrm{D}}·\frac{{\mathrm{h}}_2}{{\mathrm{h}}_1}$

Mas, para a lente ocular:

$\frac{{\mathrm{h}}_2}{{\mathrm{h}}_1}=-\frac{\mathrm{p}{\text{'}}_2}{{\mathrm{p}}_2}=-\frac{\mathrm{p}{\text{'}}_2}{{\displaystyle \frac{\mathrm{p}{\text{'}}_2·{\mathrm{f}}_2}{\mathrm{p}{\text{'}}_2-{\mathrm{f}}_2}}}=\frac{{\mathrm{f}}_2-\mathrm{p}{\text{'}}_2}{{\mathrm{f}}_2}=\frac{{\mathrm{f}}_2+\mathrm{D}}{{\mathrm{f}}_2}$

Logo:

$\mathrm{G}=\frac{{\mathrm{f}}_1}{\mathrm{D}}·\frac{{\mathrm{f}}_2+\mathrm{D}}{{\mathrm{f}}_2}\to \mathrm{G}=\frac{{\mathrm{f}}_1}{{\mathrm{f}}_2}·\left(1+\frac{{\mathrm{f}}_2}{\mathrm{D}}\right)$

Nas condições nominais: $\mathrm{D}\to \infty$

Logo: ${\mathrm{G}}_{\mathrm{N}}=\frac{{\mathrm{f}}_1}{{\mathrm{f}}_2}$

Para $\mathrm{D}\to \infty$: ${\mathrm{p}}_2={\mathrm{f}}_2$

Portanto, o comprimento do tubo é:

$\mathrm{L}={\mathrm{f}}_1+{\mathrm{p}}_2\to \mathrm{L}={\mathrm{f}}_1+{\mathrm{f}}_2$

a) Comprimento do tubo:

$\mathrm{L}={\mathrm{f}}_1+{\mathrm{f}}_2=80+5\to \boxed{\mathrm{L}=85 \mathrm{cm}}$

b) Aumento angular (em módulo):

$\mathrm{G}=\frac{{\mathrm{f}}_1}{{\mathrm{f}}_2}=\frac{80}{5}\to \boxed{\mathrm{G}=16}$

Com sinal algébrico:

$\boxed{\mathrm{G}=-16}$

A imagem é $\boxed{\mathrm{invertida}}$.

c) Objetiva:

$\mathrm{p}{\text{'}}_1=\frac{{\mathrm{p}}_1·{\mathrm{f}}_1}{{\mathrm{p}}_1-{\mathrm{f}}_1}=\frac{40·80}{40-80}\to \mathrm{p}{\text{'}}_1=-80 \mathrm{cm}$

A imagem da objetiva atua como objeto para a ocular.

Ocular:

$$\begin{gathered} {\mathrm{p}}_2=\mathrm{L}-\mathrm{p}{\text{'}}_1=85-\left(-80\right)=165 \mathrm{cm} \\ \mathrm{p}{\text{'}}_2=\frac{{\mathrm{p}}_2·{\mathrm{f}}_2}{{\mathrm{p}}_2-{\mathrm{f}}_2}=\frac{165·5}{165-5}\to \boxed{\mathrm{p}{\text{'}}_2=5,2 \mathrm{cm}} \end{gathered}$$

Aumento linear resultante:

$\mathrm{A}={\mathrm{A}}_1·{\mathrm{A}}_2=\left(-\frac{\mathrm{p}{\text{'}}_1}{{\mathrm{p}}_1}\right)·\left(-\frac{\mathrm{p}{\text{'}}_2}{{\mathrm{p}}_2}\right)=\left(\frac{\mathrm{p}{\text{'}}_1}{{\mathrm{p}}_1}\right)·\left(\frac{\mathrm{p}{\text{'}}_2}{{\mathrm{p}}_2}\right)=\left(\frac{-80}{40}\right)·\left(\frac{5,2}{165}\right)\to \mathrm{A}=-0,063$

Portanto:

A imagem é $\boxed{\mathrm{real}, \mathrm{invertida}, \mathrm{menor} \mathrm{e} \mathrm{dista} 5,2 \mathrm{cm} \mathrm{da} \mathrm{ocular}}$.