Dissertativa 3 - 2ª Fase - Dia 3 - ITA 2026

Clique aqui e veja a resolução ITA 1ª Fase 2026

Novidade! Correção inteligente - simulado seus resultados.

Selecione uma prova

Gabarito

Física
1. 1DIS
2. 2DIS
3. 3DIS
4. 4DIS
5. 5DIS
6. 6DIS
7. 7DIS
8. 8DIS
9. 9DIS
10. 10DIS

Questão ativa
Já visualizadas
Não visualizadas
Resolução pendente
ANL
Questão anulada
S/A
Sem alternativas

Questão 3

Dissertativa

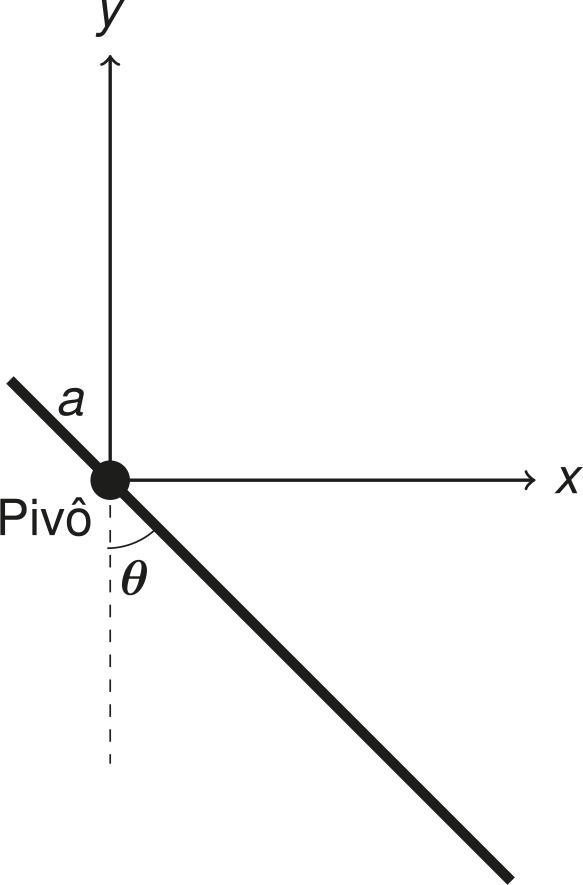
Uma haste fina e homogênea de comprimento total $L$ e massa $M$ está presa a um pivô fixo, localizado a uma distância $a$ de uma das extremidades, conforme a figura. A haste pode girar livremente em um plano vertical sob a ação da gravidade. Em determinado instante, ela gira com velocidade angular $\omega$ em torno do pivô, formando um ângulo $\theta$ com a vertical.

Dadas as considerações, calcule

a) a componente radial da força de reação exercida pelo pivô sobre a haste nesse instante, em função de $M$ , $L$ , $a$ , $\theta$ , $\omega$ e $g$ ;

b) o ângulo $\theta$ para que a componente radial da força de reação se anule, em função de $M$ , $L$ , $a$ , $\omega$ e $g$ .

Resolução:

a) Adotando o referencial girante, pode-se calcular a força centrífuga sobre cada trecho de barra (comprimentos $a$ e $L - a$ ), considerando que toda a massa desse trecho está concentrada em seu centro geométrico.

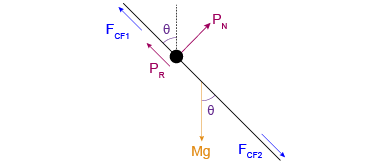
Equilíbrio na direção radial:

$F_{{cf}_{1}} + P_{R} = Mgcosθ + F_{{cf}_{2}}$

$m_{a} ω^{2} (\frac{a}{2}) + P_{R} = Mgcosθ + m_{L - a} ω^{2} (\frac{L - a}{2}) \frac{a}{L} M ω^{2} (\frac{a}{2}) + P_{R} + Mgcosθ + \frac{L - a}{L} M ω^{2} (\frac{L - a}{2}) \frac{M ω^{2}}{2 L} a^{2} + P_{R} = Mgcosθ + \frac{M ω^{2}}{2 L} {(L - a)}^{2} P_{R} = Mgcosθ + \frac{M ω^{2}}{2 L} (L^{2} - 2 La + a^{2} - a^{2}) P_{R} = Mgcosθ + \frac{M ω^{2}}{2 L} L (L - 2 a) P_{R} = Mgcosθ + \frac{M ω^{2} (L - 2 a)}{2}$

Impondo $P_{R} = 0$ :

$Mgcosθ + \frac{M ω^{2} (L - 2 a)}{2} = 0 \to θ = \arccos (- \frac{ω^{2} (L - 2 a)}{2 g})$

Obs.: com base na figura do enunciado, considerou-se $a < \frac{L}{2}$ .

Downloads

Provas

Fique por dentro das novidades

Inscreva-se em nossa newsletter para receber atualizações sobre novas resoluções, dicas de estudo e informações que vão fazer a diferença na sua preparação!