Dissertativa 2 - 2ª Fase - Dia 3 - ITA 2026

Novidade! Correção inteligente - simulado seus resultados.

Clique aqui e veja a resolução ITA 1ª Fase 2026

Selecione uma prova

Gabarito

Física
1. 1DIS
2. 2DIS
3. 3DIS
4. 4DIS
5. 5DIS
6. 6DIS
7. 7DIS
8. 8DIS
9. 9DIS
10. 10DIS

Questão ativa
Já visualizadas
Não visualizadas
Resolução pendente
ANL
Questão anulada
S/A
Sem alternativas

Questão 2

Dissertativa

Uma barra rígida, homogênea e uniforme, de massa M e comprimento L, possui dois apoios fixos, A e B, que estão em contato com um plano inclinado que forma um ângulo $θ$ com a horizontal. Os pontos de contato com o plano inclinado estão localizados a uma distância d de cada extremidade da barra, conforme ilustrado na figura. Um objeto de massa m está preso à barra a uma distância $a$ da extremidade inferior. Para manter o equilíbrio, um contrapeso de massa $m_{c}$ é acoplado a uma distância b da extremidade superior da barra. Admita que os apoios sofrem forças de atrito estático.

Considerando que a barra permanece em repouso, faça o que se pede nos itens a seguir, expressando as respostas em termos dos parâmetros dados (M, m, $m_{c}$ , L, d, a, b, g, $θ$ ).

a) Determine o valor das forças normais exercidas sobre os apoios A e B.

b) Calcule a força de atrito em cada apoio, que impeça o deslizamento da barra ao longo do plano.

Resolução:

a) A figura a seguir ilustra o diagrama de corpo livre:

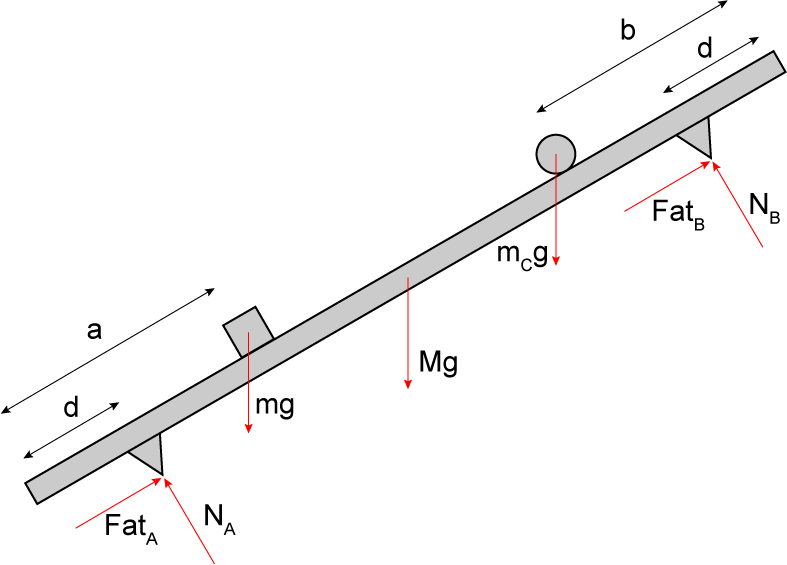
Equilíbrio de momentos em relação ao apoio A:

$\sum M_{A} = 0 \Rightarrow N_{B} \cdot (L - 2 d) = [m \cdot (a - d) + M \cdot (\frac{L}{2} - d) + m_{C} \cdot (L - b - d)] \cdot gcosθ$

$N_{B} = \frac{[m \cdot (a - d) + M \cdot (\frac{L}{2} - d) + m_{C} \cdot (L - b - d)] \cdot gcosθ}{(L - 2 d)}$

Equilíbrio de momentos em relação ao apoio B:

$\sum M_{B} = 0 \Rightarrow N_{A} \cdot (L - 2 d) = [m \cdot (L - a - d) + M \cdot (\frac{L}{2} - d) + m_{C} \cdot (b - d)] \cdot gcosθ$

$N_{A} = \frac{[m \cdot (L - a - d) + M \cdot (\frac{L}{2} - d) + m_{C} \cdot (b - d)] \cdot gcosθ}{(L - 2 d)}$

b) Do equilíbrio de forças na direção paralela ao plano:

$\sum F_{x} = 0 \Rightarrow {Fat}_{A} + {Fat}_{B} = (m + M + m_{C}) \cdot g sen θ$

Observação: Não há dados suficientes para calcular as forças de atrito em cada apoio, apenas a soma delas.

Downloads

Provas

Fique por dentro das novidades

Inscreva-se em nossa newsletter para receber atualizações sobre novas resoluções, dicas de estudo e informações que vão fazer a diferença na sua preparação!