Dissertativa 1 - 2ª Fase - Dia 3 - ITA 2026

Clique aqui e veja a resolução ITA 1ª Fase 2026

Novidade! Correção inteligente - simulado seus resultados.

Selecione uma prova

Gabarito

Física
1. 1DIS
2. 2DIS
3. 3DIS
4. 4DIS
5. 5DIS
6. 6DIS
7. 7DIS
8. 8DIS
9. 9DIS
10. 10DIS

Questão ativa
Já visualizadas
Não visualizadas
Resolução pendente
ANL
Questão anulada
S/A
Sem alternativas

Questão 1

Dissertativa

Um trem de massa M desloca-se a uma velocidade constante v sobre trilhos horizontais. Para garantir a aderência em curvas, as rodas do trem possuem formato de tronco de cone regular com ângulo $θ$ com a horizontal, conforme se observa na figura. Considerando que o raio de curvatura é muito maior que as dimensões do trem e que o eixo das rodas permanece na horizontal, calcule o raio de curvatura mínimo para que nenhuma das rodas perca o contato com o trilho nas seguintes situações:

a) quando o coeficiente de atrito estático entre as rodas e o trilho é $μ$ ;

b) quando o atrito é desprezível;

c) quando o coeficiente de atrito estático é $μ$ e as rodas são cilíndricas.

Resolução:

a) Equilíbrio do trem no referencial girante:

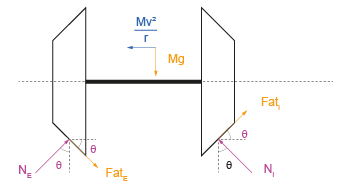
Se a força centrífuga for suficientemente grande, haverá perda de contato no trilho interno. Na iminência de isso acontecer, $N_{i} \approx 0$ e ${Fat}_{i} \approx 0$ .

Equilíbrio translacional do trem:

$N_{E} senθ + {Fat}_{E} cosθ = \frac{{Mv}^{2}}{r} (I) N_{E} cosθ - {Fat}_{E} senθ = Mg (II)$

$(I) \div (II)$ :

$\frac{N_{E} senθ + {Fat}_{E} cosθ}{N_{E} cosθ - {Fat}_{E} senθ} = \frac{v^{2}}{rg}$

Na condição limite, ${Fat}_{E} = {μN}_{E}$ :

$\frac{N_{E} senθ + {μN}_{E} cosθ}{N_{E} cosθ - μ n_{E} senθ} = \frac{v^{2}}{rg} \Rightarrow r = \frac{v^{2}}{g} \frac{cosθ - μsenθ}{senθ + μcosθ}$

b) Impondo-se $μ = 0$ : $r = \frac{v^{2}}{g} cotgθ$

c) Impondo-se $θ = 0$ : $r = \frac{v^{2}}{g} \frac{1 - μ \cdot 0}{0 + μ \cdot 1} \Rightarrow r = \frac{v^{2}}{μg}$

Downloads

Provas

Fique por dentro das novidades

Inscreva-se em nossa newsletter para receber atualizações sobre novas resoluções, dicas de estudo e informações que vão fazer a diferença na sua preparação!