Questão 156 - Dia 2 - Amarelo - Enem 2025

Novidade! Correção inteligente - simulado seus resultados.

Assista agora ao Poliedro Resolve do 1º dia do Enem 2025

Selecione uma prova

Gabarito

Geral
1. 91C
2. 92B
3. 93D
4. 94D
5. 95C
6. 96D
7. 97A
8. 98E
9. 99A
10. 100A
11. 101A
12. 102E
13. 103C
14. 104B
15. 105B
16. 106C
17. 107E
18. 108A
19. 109E
20. 110E
21. 111B
22. 112D
23. 113E
24. 114E
25. 115C
26. 116A
27. 117B
28. 118B
29. 119B
30. 120D
31. 121E
32. 122C
33. 123D
34. 124C
35. 125B
36. 126B
37. 127B
38. 128D
39. 129C
40. 130E
41. 131A
42. 132D
43. 133D
44. 134C
45. 135D
46. 136C
47. 137E
48. 138C
49. 139C
50. 140A
51. 141D
52. 142D
53. 143B
54. 144E
55. 145B
56. 146C
57. 147A
58. 148C
59. 149E
60. 150C
61. 151B
62. 152D
63. 153D
64. 154D
65. 155B
66. 156A
67. 157D
68. 158E
69. 159E
70. 160A
71. 161B
72. 162B
73. 163E
74. 164C
75. 165C
76. 166D
77. 167A
78. 168B
79. 169E
80. 170A
81. 171D
82. 172D
83. 173E
84. 174B
85. 175E
86. 176AD
87. 177A
88. 178B
89. 179C
90. 180C

Questão ativa
Já visualizadas
Não visualizadas
Resolução pendente
ANL
Questão anulada
S/A
Sem alternativas

Questão 156

Objetiva

156

O dono de uma embarcação deve partir do ponto $P$ e chegar ao ponto $R$ por meio de dois deslocamentos lineares e navegando a uma velocidade constante. Essa viagem será feita durante a noite, e como ele dispõe somente de uma bússola e de um relógio, planejou sua rota da seguinte forma:

1º – partir do ponto $P$ na direção 110 e navegar por 4 horas, alcançando um ponto $Q$ ;

2º – partir do ponto $Q$ na direção 90 e navegar por 2 horas, alcançando o ponto de destino $R$ .

No entanto, ao direcionar o barco para o primeiro deslocamento, o fez na direção 340, em vez de 110. Com isso, realizou os seguintes deslocamentos:

1º – partiu do ponto $P$ na direção 340 e navegou por 4 horas, alcançando um ponto $S$ ;

2º – partiu do ponto $S$ na direção 90 e navegou por 2 horas, alcançando o ponto $T$ .

A figura apresenta a bússola, a rota planejada e a rota executada.

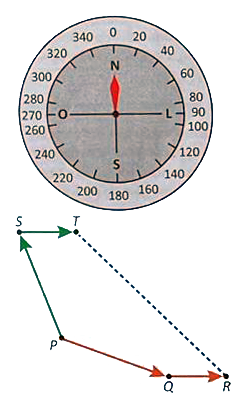
O dono da embarcação só percebeu o equívoco ao chegar ao ponto $T$ . Com isso, agora ele precisa definir a direção e o tempo de navegação que lhe permita, partindo do ponto $T$ , chegar ao ponto de destino $R$ por meio de uma rota retilínea.

Considere 0,64 como aproximação para $\cos 50 °$ .

A direção e o tempo aproximado de navegação que o dono da embarcação deve utilizar são, respectivamente,

Alternativas

A
135 e 7 horas e 15 minutos.
B
45 e 7 horas e 15 minutos.
C
135 e 12 horas.
D
135 e 6 horas.
E
45 e 6 horas.

Gabarito:
A

Para seguir do ponto $P$ para o ponto $Q$ , houve uma rotação de 110° no sentido horário, e para seguir do ponto $P$ para o ponto $S$ , houve uma rotação de 20° no sentido anti-horário.

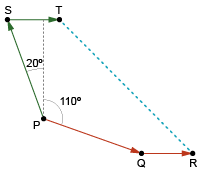
Traçando um segmento de reta de $S$ até $Q$ , forma-se o triângulo isósceles SPQ e o paralelogramo SQRT, conforme a figura a seguir.

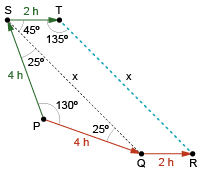
Pela lei dos cossenos no triângulo SPQ e como $\cos 130 º = - \cos 50 º = - 0, 64,$ tem-se:

$x^{2} = 4^{2} + 4^{2} - 2 \cdot 4 \cdot 4 \cdot \cos 130 º x^{2} = 16 + 16 - 32 \cdot (- \cos 50 º) x^{2} = 32 - 32 \cdot (- 0, 64) x^{2} = 32 + 20, 48 x^{2} = 52, 48 x \approx 7, 25 h$

Portanto, a direção para partir do ponto $P$ e chegar ao ponto $T$ deve ser 135 e o tempo de navegação é de, aproximadamente, 7,25 h, ou seja, 7 horas e 15 minutos.

Observação: Para calcular $x = \sqrt{52, 48} = \sqrt{\frac{5248}{100}}$ , ao fatorar 5248, percebe-se que:

Então, $\sqrt{5248} = 2 \cdot 2 \cdot 2 \cdot \sqrt{82}$ , como $\sqrt{82}$ não é exata, mas é muito próxima da raiz quadrada de 81 que vale 9, então, $\sqrt{5248} \approx 8 \cdot 9 = 72$ . Assim, $x = \sqrt{\frac{5248}{100}} \approx \frac{72}{10} = 7, 2$ .

Para assinalar a alternativa, o estudante poderia notar que 52,48 é um número entre 49 e 64, ou seja, sua raiz quadrada deve estar entre 7 e 8 e a única alternativa que contém um número para o tempo de percurso nessas condições é a alternativa A.

156

Downloads

Provas

Fique por dentro das novidades

Inscreva-se em nossa newsletter para receber atualizações sobre novas resoluções, dicas de estudo e informações que vão fazer a diferença na sua preparação!