Fique por dentro das novidades
Inscreva-se em nossa newsletter para receber atualizações sobre novas resoluções, dicas de estudo e informações que vão fazer a diferença na sua preparação!
Dissertativas 4 - 1ª Fase - Einstein 2025
Gabarito
Um dado comum é o objeto obtido pela inscrição dos números 1, 2, 3, 4, 5 e 6 nas faces de um cubo, de modo que a soma dos números em faces opostas resulte sempre no mesmo número. A figura mostra uma planificação de um dado comum.
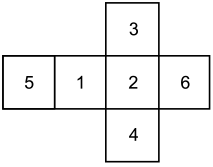
Um dado incomum será definido como o objeto obtido pela inscrição dos números – 4, – 3, – 2, – 1, 0 e 1 nas faces de um cubo, de modo que a soma dos números em faces opostas resulte sempre no mesmo número.
a) A figura mostra uma planificação de um dado com apenas uma face já inscrita com o número 1.
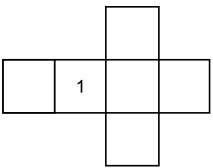
De quantas maneiras distintas é possível inscrever os outros cinco números na planificação indicada de modo a ser uma planificação de um dado incomum?
b) Calcule a probabilidade de, em um lançamento simultâneo de dois dados, sendo um comum e o outro incomum, a soma dos números inscritos nas faces superiores dos dados ser estritamente positiva.
Resolução:
Resolução:
a) Nas faces opostas, têm-se os seguintes pares de números: –4 e 1, –2 e –1, –3 e 0. Assim, como já se tem a posição do número 1, também tem-se a posição do –4.
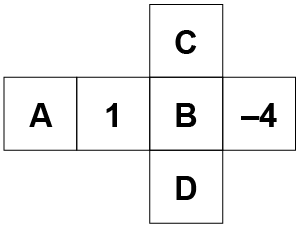
Para a posição “A”, têm-se quatro possibilidades (os outros números) que fixam a posição “B” em apenas uma opção. Dessa forma, sobram duas possibilidades para a posição “C” e o último número vai para a posição “D”. Logo há = 8 opções para a planificação do dado.
Observação: independentemente da planificação escolhida, sempre tem-se o mesmo dado quando o hexaedro regular é montado.
b) Lançando os dois dados, têm-se 36 resultados possíveis e, desses, 26 estritamente positivos:
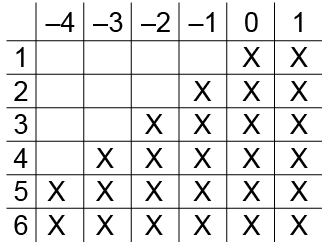
Portanto, a probabilidade pedida é .
Downloads
Provas