Dissertativa 15 - Conhecimentos Específicos e Redação - Santa Casa 2026

Novidade! Correção inteligente - simulado seus resultados.

Selecione uma prova

Gabarito

Medicina
1. 1DIS
2. 2DIS
3. 3DIS
4. 4DIS
5. 5DIS
6. 6DIS
7. 7DIS
8. 8DIS
9. 9DIS
10. 10DIS
11. 11DIS
12. 12DIS
13. 13DIS
14. 14DIS
15. 15DIS
16. 16DIS
17. 17DIS
18. 18DIS
19. 19DIS
20. 20DIS
21. REDRED

Questão ativa
Já visualizadas
Não visualizadas
Resolução pendente
ANL
Questão anulada
S/A
Sem alternativas

Questão 15

Dissertativa

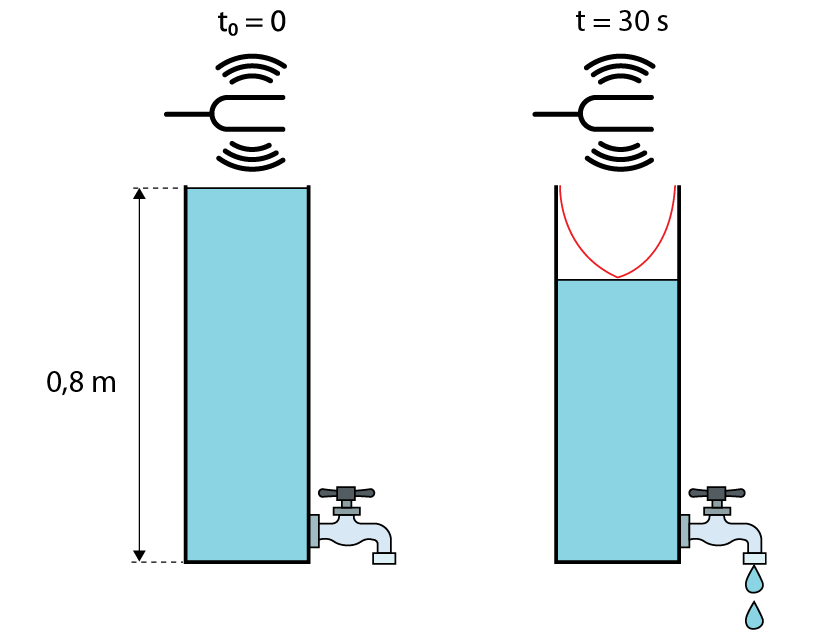
Um recipiente cilíndrico de altura 0,8 m e com área da base medindo $3 x 10^{- 2} m^{2}$ está inicialmente cheio de água. No fundo desse recipiente, há uma torneira inicialmente fechada que, quando aberta, faz com que a água escoe lentamente com uma vazão constante de $2 x 10^{- 4} m^{3} / s$ . No instante $t_{0} = 0$ , um diapasão é colocado para vibrar com frequência f próximo à superfície da água e, simultaneamente, a torneira é aberta. No instante t = 30 s nota-se que a coluna de ar dentro do recipiente entra, pela primeira vez, em ressonância com o som emitido pelo diapasão, produzindo ondas sonoras com a frequência do modo fundamental de vibração (primeiro harmônico), como mostra a figura.

a) Calcule o volume de água, em $m^{3}$ , que deve escoar pela torneira para que a pressão exercida apenas pela água no fundo desse recipiente cilíndrico seja reduzida à metade do valor inicial.

b) Considerando a velocidade do som no ar dentro desse recipiente cilíndrico igual a 340 m/s, calcule a frequência, em Hz, do som emitido pelo diapasão.

Resolução:

a) Com base na equação de Stevin, a pressão hidrostática é dada por: $P = d \cdot g \cdot H$ .

Para que a pressão exercida apenas pela coluna de água caia pela metade, a altura da coluna deverá ser reduzida à metade, ou seja:

$P' = \frac{P}{2} \Rightarrow d \cdot g \cdot H' = \frac{d \cdot g \cdot H}{2} \Rightarrow H' = \frac{H}{2} \Rightarrow H' = 0, 4 m$

Logo, o volume que escoa por ser obtido por:

$ΔV = A \cdot H' \Rightarrow ΔV = 3 \cdot 10^{- 2} \cdot 0, 4 \Rightarrow ΔV = 1, 2 \cdot 10^{- 3} m^{3}$

b) No intervalo de 30 s, o volume de líquido que escoa é:

$Z = \frac{ΔV}{Δt} \Rightarrow 2 \cdot 10^{- 4} = \frac{ΔV}{30} \Rightarrow ΔV = 6 \cdot 10^{- 3} m^{3}$

A altura da coluna de líquido que desce é a mesma altura da coluna de ar que se forma. Logo, tem-se:

$ΔV = A \cdot ΔH \Rightarrow 6 \cdot 10^{- 3} = 3 \cdot 10^{- 2} \cdot ΔH \Rightarrow ΔH = 0, 2 m$

Como nessa coluna de ar, forma-se o harmônico fundamental do tubo fechado, tem-se:

$ΔH = \frac{λ}{4} \Rightarrow λ = 4 \cdot ΔH \Rightarrow λ = 0, 8 m$

Aplicando-se esse resultado na equação fundamental das ondas:

$v = λ \cdot f \Rightarrow 340 = 0, 8 \cdot f \Rightarrow f = 425 Hz$

Downloads

Provas

Fique por dentro das novidades

Inscreva-se em nossa newsletter para receber atualizações sobre novas resoluções, dicas de estudo e informações que vão fazer a diferença na sua preparação!