Dissertativa 7 - 2ª Fase - Dia 1 - ITA 2026

Seja $\mathrm{a}\in \mathrm{ℝ}$ o coeficiente líder de p(x).

Desse modo, p(x) = ${\mathrm{ax}}^4+{\mathrm{bx}}^3+{\mathrm{cx}}^2+\mathrm{dx}+\mathrm{e}$, em que a, b, c, d, e$\in \mathrm{ℝ}$.

Das relações de Girard, têm-se:

${\mathrm{x}}_1+{\mathrm{x}}_2+{\mathrm{x}}_3+{\mathrm{x}}_4=-\frac{\mathrm{b}}{\mathrm{a}}\Rightarrow \frac{3}{2}=-\frac{\mathrm{b}}{\mathrm{a}}\Rightarrow \mathrm{b}=-\frac{3\mathrm{a}}{2}$

${\mathrm{x}}_1·{\mathrm{x}}_2·{\mathrm{x}}_3·{\mathrm{x}}_4=\frac{\mathrm{e}}{\mathrm{a}}\Rightarrow -\frac{5}{2}=\frac{\mathrm{e}}{\mathrm{a}}\Rightarrow \mathrm{e}=-\frac{5\mathrm{a}}{2}$

Assim, p(x) pode ser reescrito como:

$\mathrm{p}\left(\mathrm{x}\right)={\mathrm{ax}}^4-\frac{3}{2}{\mathrm{ax}}^3+{\mathrm{cx}}^2+\mathrm{dx}-\frac{5\mathrm{a}}{2}$

Pelo algoritmo da divisão:

$\mathrm{p}\left(\mathrm{x}\right)\equiv \left({\mathrm{x}}^3-\mathrm{x}+4\right)\mathrm{q}\left(\mathrm{x}\right)+9{\mathrm{x}}^2-4\mathrm{x}+7$

Como p(x) é de grau 4, q(x) deve ser de grau 1. Como o coeficiente líder de p(x) é a, tem-se que q(x) = ax + n. Assim:

$\mathrm{p}\left(\mathrm{x}\right)\equiv \left({\mathrm{x}}^3-\mathrm{x}+4\right)\left(\mathrm{ax}+\mathrm{n}\right)+9{\mathrm{x}}^2-4\mathrm{x}+7$

Desenvolvendo os termos:

$\mathrm{p}\left(\mathrm{x}\right)\equiv {\mathrm{ax}}^4+{\mathrm{nx}}^3+\left(9-\mathrm{a}\right){\mathrm{x}}^2+\left(4\mathrm{a}-\mathrm{n}-4\right)\mathrm{x}+\left(4\mathrm{n}+7\right)$

Portanto, por identidade polinomial:

$\left\{\begin{array}{l}-\frac{3}{2}\mathrm{a}=\mathrm{n}\\ \mathrm{c}=9-\mathrm{a}\\ \mathrm{d}=4\mathrm{a}-\mathrm{n}-4\\ -\frac{5}{2}\mathrm{a}=4\mathrm{n}+7\end{array}\right.$

Resolvendo o sistema:

a = 2, c = 7, d = 7, n =$-3$

Desse modo:

$\mathrm{p}\left(\mathrm{x}\right)=2{\mathrm{x}}^4-3{\mathrm{x}}^3+7{\mathrm{x}}^2+7\mathrm{x}-5$

Por inspeção, nota-se que $-1$ é raiz. Por Briot–Ruffini:

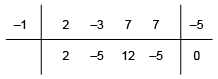
Por inspeção de raízes racionais, $\frac{1}{2}$ é raiz de $2{\mathrm{x}}^3-5{\mathrm{x}}^2+12\mathrm{x}-5=0$. Novamente, efetuando a divisão:

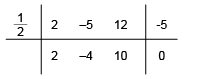
Por fim, as raízes de $2{\mathrm{x}}^2-4\mathrm{x}+10=0$ são $1\pm 2\mathrm{i}$.

Desse modo, as raízes de p(x) são $\boxed{-1,\frac{1}{2},1+2\mathrm{i},1-2\mathrm{i}}$.