Dissertativa 5 - 2ª Fase - Dia 1 - ITA 2026

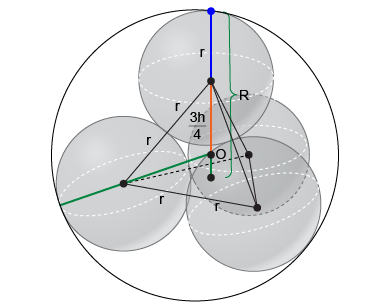
Sejam r o raio das esferas menores e R o raio da esfera maior. Os centros das esferas menores formam um tetraedro regular de aresta 2r. O centro O do tetraedro regular também é o centro da esfera maior, localizando-se no encontro das alturas do tetraedro e as dividindo na razão 3:1.

Assim:

$\mathrm{R}=\mathrm{r}+\frac{3}{4}\mathrm{h}=\mathrm{r}+\frac{3}{4}2\mathrm{r}\frac{\sqrt{6}}{3}=\mathrm{r}\left(1+\frac{\sqrt{6}}{2}\right)$

A razão entre o volume da esfera maior e a soma dos volumes das esferas menores é dada por:

$\frac{{\displaystyle \frac{4}{3}{\mathrm{\pi R}}^3}}{4·{\displaystyle \frac{4}{3}}{\mathrm{\pi r}}^3}=\frac{1}{4}{\left(\frac{\mathrm{R}}{\mathrm{r}}\right)}^3=\frac{1}{4}{\left(1+\frac{\sqrt{6}}{2}\right)}^3=\boxed{\frac{22+9\sqrt{6}}{16}}$