Fique por dentro das novidades
Inscreva-se em nossa newsletter para receber atualizações sobre novas resoluções, dicas de estudo e informações que vão fazer a diferença na sua preparação!

As diagonais do parelelogramo ABCD estão contidas nas retas e . As retas r e s se encontram no ponto X. Sabendo que C = (8,5) e que a equação da circunferência inscrita no triângulo ABX é
determine a área de ABCD.
(i) Encontrando o ponto X, interseção das diagonais:
(ii) X é o ponto médio da diagonal . Logo:
Assim: .
(iii) Sejam I o centro e r o raio da circunferência inscrita em AXB:
.
(iv) Os coeficientes angulares de r e s são, respectivamente, e . Assim, o ângulo agudo que ambas fazem com a horizontal tem tangente igual a .
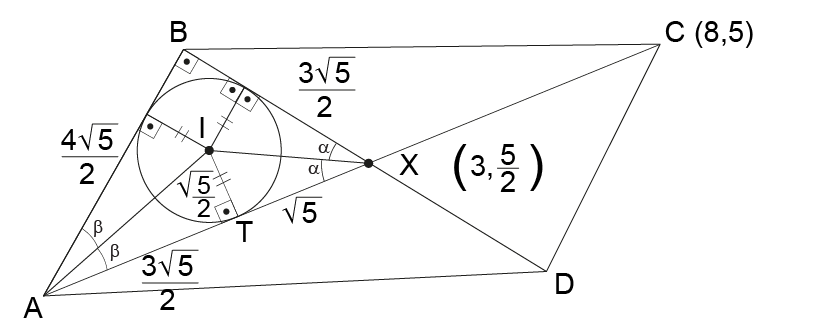
Da figura, é paralela ao eixo x e:
No triângulo ITX:
(i) Encontrando o ponto X, interseção das diagonais:
(ii) X é o ponto médio da diagonal . Logo:
Assim: .
Nota-se que há duas tangentes que partem de A e tocam na circunferência inscrita em ABX. A equação geral dessas tangentes é da forma:
Como a distância do centro da circunferência até a reta tangente deve ser igual ao raio, tem-se:
Como, para , já tem-se a reta r, a outra tangente será: .
Nota-se que o ponto B é a solução de
Logo, a área de ABX é:
Como
Inscreva-se em nossa newsletter para receber atualizações sobre novas resoluções, dicas de estudo e informações que vão fazer a diferença na sua preparação!