Questão 48 - Unicamp - Q e X - Unicamp 2026

Novidade! Correção inteligente - simulado seus resultados.

Selecione uma prova

Gabarito

Geral
1. 1C
2. 2B
3. 3C
4. 4B
5. 5D
6. 6C
7. 7D
8. 8D
9. 9C
10. 10B
11. 11C
12. 12A
13. 13A
14. 14B
15. 15A
16. 16C
17. 17D
18. 18D
19. 19A
20. 20A
21. 21B
22. 22D
23. 23D
24. 24C
25. 25C
26. 26D
27. 27B
28. 28C
29. 29D
30. 30B
31. 31C
32. 32A
33. 33B
34. 34B
35. 35A
36. 36D
37. 37C
38. 38C
39. 39B
40. 40D
41. 41C
42. 42C
43. 43A
44. 44D
45. 45B
46. 46C
47. 47D
48. 48C
49. 49B
50. 50A
51. 51C
52. 52B
53. 53A
54. 54B
55. 55A
56. 56C
57. 57A
58. 58D
59. 59C
60. 60B
61. 61D
62. 62A
63. 63B
64. 64D
65. 65C
66. 66D
67. 67B
68. 68C
69. 69B
70. 70A
71. 71A
72. 72D

Questão ativa
Já visualizadas
Não visualizadas
Resolução pendente
ANL
Questão anulada
S/A
Sem alternativas

Questão 48

Objetiva

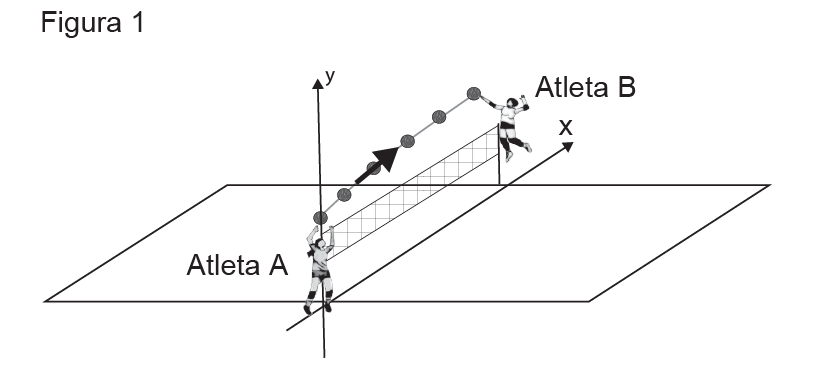
O movimento de ataque em um jogo de voleibol é mais eficiente se o atleta atingir a bola no ponto mais alto da trajetória do centro de massa da bola. A Figura 1 mostra a trajetória da bola que foi lançada pela Atleta A em direção à Atleta B.

O centro de massa da bola, ao ser lançada pela Atleta A, está a 2 metros de altura em relação ao solo. Quando a Atleta B ataca, o centro de massa da bola está a 3 metros de altura em relação ao solo.

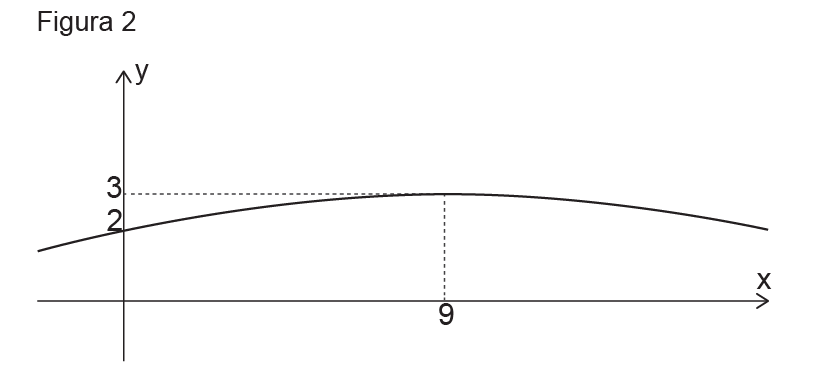
As jogadoras estão no mesmo plano da trajetória da bola e a distância entre as jogadoras é de 9 metros. Sabe-se que a trajetória do centro de massa da bola é uma parábola e que o ataque aconteceu justamente no ponto de maior altura da parábola, conforme representado na Figura 2.

A equação da parábola que descreve a trajetória do centro de massa da bola é

Alternativas

A
$y = (- 1 / 9) x^{2} + (10 / 9) x + 2$ .
B
$y = (- 1 / 99) x^{2} + (20 / 99) x + 2$ .
C
$y = (- 1 / 81) x^{2} + (2 / 9) x + 2$ .
D
$y = (- 1 / 4) x^{2} + (9 / 2) x + 2$ .

Gabarito:
C

A parábola é o gráfico de uma função do segundo grau da forma $y = {ax}^{2} + bx + c$ e passa pelos pontos (0, 2) e (9, 3).

Como o ponto (9, 3) é o vértice da parábola e seu eixo de simetria é uma reta que passa por este ponto de modo que é paralela ao eixo y, conclui-se que um outro ponto desta parábola é (18, 2).

(0, 2) pertence à parábola: $2 = a \cdot 0^{2} + b \cdot 0 + c \Rightarrow c = 2$ . Assim, $y = {ax}^{2} + bx + 2$ .
(9, 3) pertence à parábola: $3 = a \cdot 9^{2} + b \cdot 9 + 2 \Rightarrow 81 a + 9 b = 1$ (I)
(18, 2) pertence à parábola: $2 = a \cdot 18^{2} + b \cdot 18 + 2 \Rightarrow 324 a + 18 b = 0$ (II)

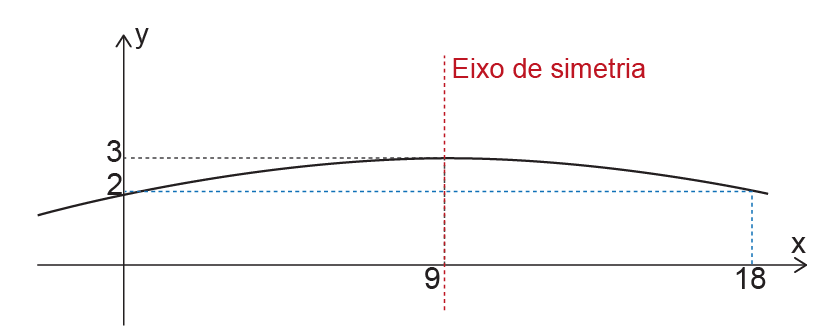
Da equação (II) vê-se que $18 b = - 324 a \Rightarrow b = - 18 a$ .

Substituindo na equação (I), conclui-se que $81 a + 9 \cdot (- 18 a) = 1 \Rightarrow a = - \frac{1}{81}$ e voltando em (II), tem-se $b = \frac{2}{9}$ .

Portanto, $y = (- \frac{1}{81}) x^{2} + (\frac{2}{9}) x + 2$ .

Downloads

Provas

Fique por dentro das novidades

Inscreva-se em nossa newsletter para receber atualizações sobre novas resoluções, dicas de estudo e informações que vão fazer a diferença na sua preparação!