Dissertativas 24 - 2ª Fase - Dia 1 - Unesp 2025

a. Sendo g(x) = 4x – $\frac{{\mathrm{x}}^2}{2}$, tem-se:

$$\begin{gathered} {\mathrm{x}}_{\mathrm{V}}=\frac{-\mathrm{b}}{2\mathrm{a}}=\frac{-4}{2·\left({\displaystyle \frac{-1}{2}}\right)}=\frac{-4}{-1}=4 \\ {\mathrm{y}}_{\mathrm{V}}=\mathrm{g}\left(4\right)=4·4-\frac{4^2}{2}=16-8=8 \end{gathered}$$

Portanto, o vértice dessa parábola tem coordenadas (4, 8) e a reta r passa pelos pontos (–2, 2) e (4, 8):

$$\begin{gathered} {\mathrm{m}}_{\mathrm{r}}=\frac{∆\mathrm{y}}{∆\mathrm{x}}=\frac{8-2}{4-\left(-2\right)}=\frac{6}{6}=1 \\ \mathrm{tg} \mathrm{\theta }={\mathrm{m}}_{\mathrm{r}}=1 \end{gathered}$$

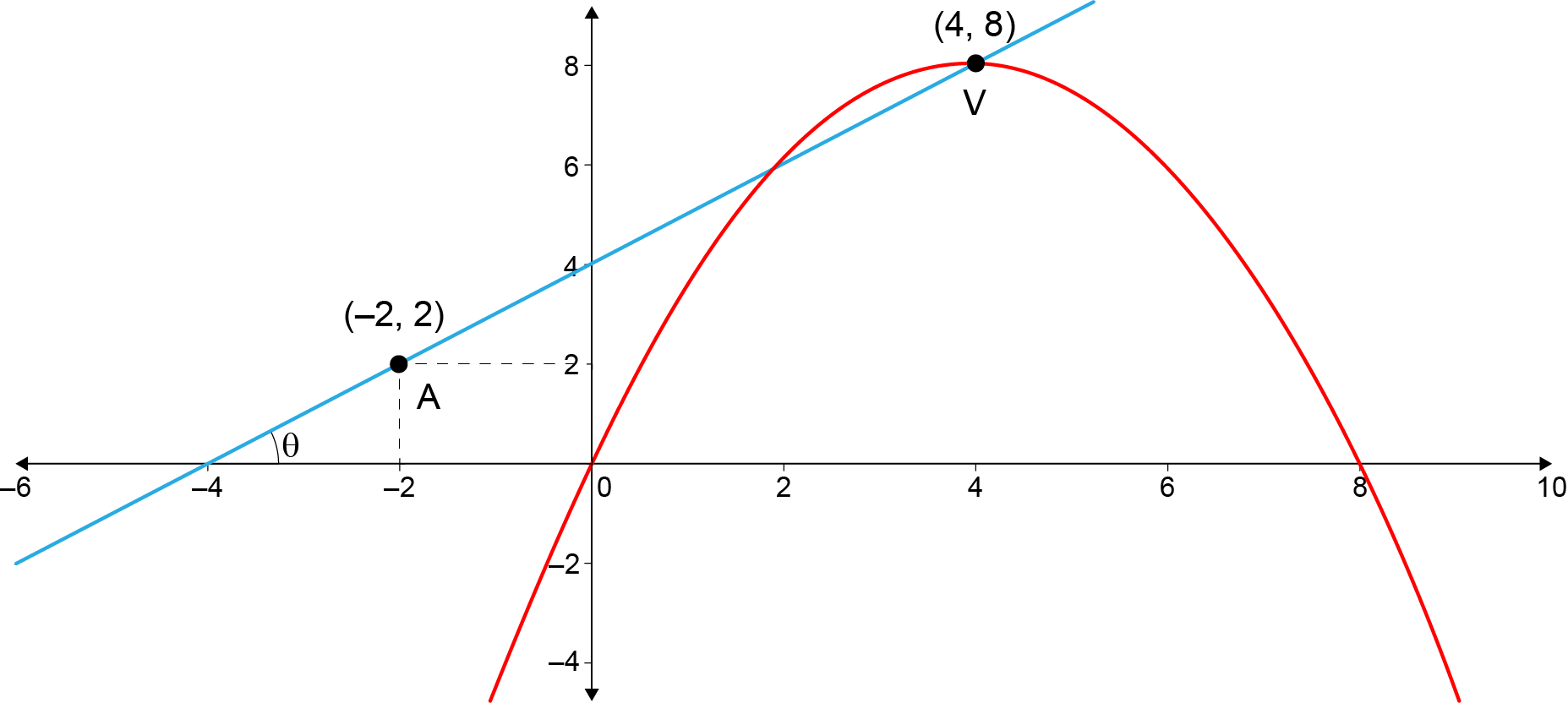
Como $\mathrm{\theta }$ é um ângulo agudo com tangente igual a 1, tem-se: $\boxed{\mathrm{\theta } = 45°}$.

b. $\mathrm{g}\left(\mathrm{x}\right)=4\mathrm{x}-\frac{{\mathrm{x}}^2}{2}=\mathrm{x}·\left(4-\frac{\mathrm{x}}{2}\right)$. Portanto, as raízes da parábola são:

$\begin{array}{c}\mathrm{x}=0\\ \mathrm{ou}\\ 4-\frac{\mathrm{x}}{2}=0\Rightarrow \mathrm{x}=8\end{array}$

Ou seja, os valores positivos de x que resultam em valores positivos de y estão entre 1 e 7.

$\mathrm{y}=\mathrm{x}·\left(4-\frac{\mathrm{x}}{2}\right)$. Portanto, para que y seja inteiro, x precisa ser par. Com isso, encontra-se que os possíveis valores de x são 2, 4 e 6, resultando nos pontos:

$\boxed{(2, 6), (4, 8) e (6, 6)}$.