Dissertativas 23 - 2ª Fase - Dia 1 - Unesp 2025

Selecione uma prova

Gabarito

Geral
1. 1DIS
2. 2DIS
3. 3DIS
4. 4DIS
5. 5DIS
6. 6DIS
7. 9DIS
8. 10DIS
9. 11DIS
10. 12DIS
11. 14DIS
12. 15DIS
13. 16DIS
14. 17DIS
15. 20DIS
16. 21DIS
17. 22DIS
18. 23DIS
19. 24DIS

Questão ativa
Já visualizadas
Não visualizadas
Resolução pendente
ANL
Questão anulada
S/A
Sem alternativas

Questão 23

Dissertativa

O centro do círculo branco indicado na figura divide a altura relativa à base $BC$ do triângulo isósceles ABC, com AB=AC, em dois segmentos de reta: um de 5 cm e outro de 3 cm. Na figura há, ainda, um setor circular de centro A e arco $\overset{⏜}{BC}$ .

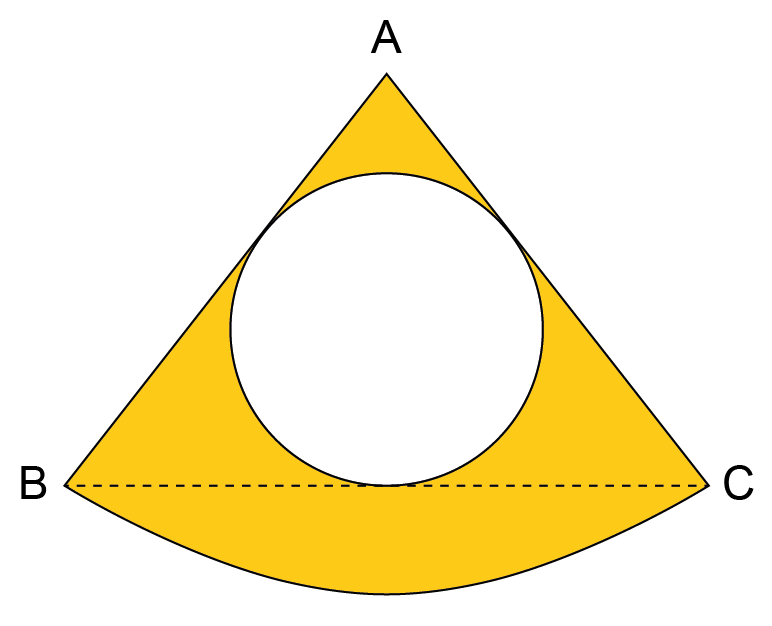
a) Calcule o perímetro do triângulo ABC, que circunscreve o círculo branco.

b) Adotando sen 53,13º = 0,8 e $π$ = 3,14, calcule, em ${cm}^{2}$ , a melhor aproximação inteira da medida da área da região indicada em amarelo na figura.

Resolução:

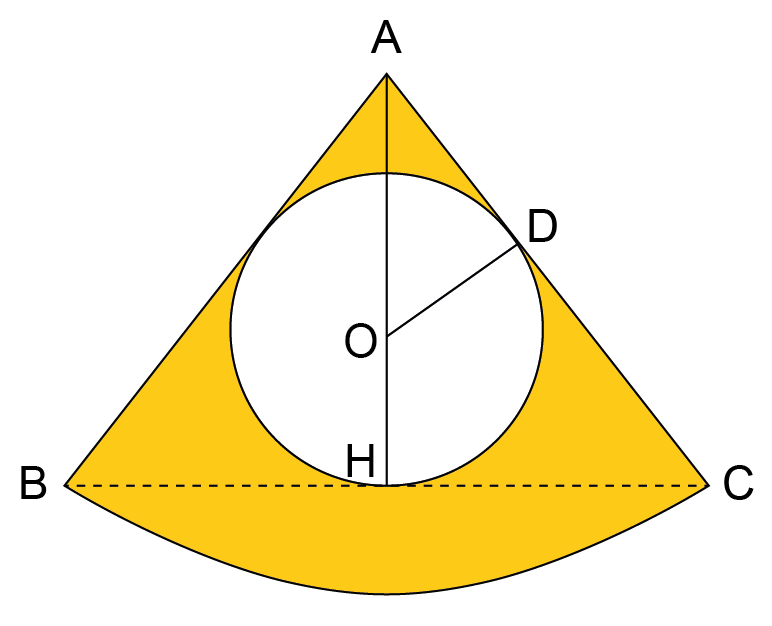
Do enunciado, AO = 5 cm e OH = 3 cm. Como OH é raio, OD = OH = 3 cm. Note que o triângulo AOD é retângulo, com um cateto igual a 3 cm e hipotenusa igual a 5 cm. Logo, AD = 4 cm (pelo teorema de Pitágoras ou lembrando da terna pitagórica).

Percebe-se que $H \hat{A} C = D \hat{A} O$ e que $\hat{D} = \hat{H} = 90 °$ . Logo, os triângulos HAC e DAO são semelhantes. Como AH = 8 cm e AD = 4 cm, a razão de semelhança é 2:1. Portanto, HC = 6 cm e AC = 10 cm. Pela simetria da figura, AC = AB e HC = HB. Logo, o perímetro P do triângulo ABC é:

$P = 10 + 10 + 12 = 32 cm$

b. Note que sen 53,13° = 0,8 = $\frac{AH}{AC}$ . Logo, $A \hat{C} B = A \hat{B} C = 53, 13 °$ e $B \hat{A} C = 73, 74 °$ .

A área desejada A equivale à área do setor $A_{s}$ menos a área do círculo $A_{c}$ :

$A = A_{s} - A_{c} A = \frac{α}{360} {πR}^{2} - {πr}^{2} A = \frac{73, 74}{360} \cdot 3, 14 \cdot 10^{2} - 3, 14 \cdot 3^{2} A = 36, 0576 ≅ 36 {cm}^{2}$

Downloads

Provas

Fique por dentro das novidades

Inscreva-se em nossa newsletter para receber atualizações sobre novas resoluções, dicas de estudo e informações que vão fazer a diferença na sua preparação!